|
Question 623675: What are the vertices of the ellipse given by the equation x2 + 4y2 + 10x – 56y + 205 = 0?
?
Found 2 solutions by ewatrrr, math-vortex:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi,
x2 + 4y2 + 10x – 56y = -205 |completing the Square
(x+5)^2 + 4(y-7)^2 = -205 + 25 + 196 = 16
C(-5,7) and V(-1,7),V(-9,7) & V(-5,9), V(-5,5)
See below descriptions of various conics
Standard Form of an Equation of a Circle is 
where Pt(h,k) is the center and r is the radius
Standard Form of an Equation of an Ellipse is 
where Pt(h,k) is the center. (a variable positioned to correspond with major axis)
a and b are the respective vertices distances from center
and ±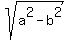 are the foci distances from center: a > b
Standard Form of an Equation of an Hyperbola opening right and left is:
 with C(h,k) and vertices 'a' units right and left of center
Foci are  units right and left of center along y = k
& Asymptote Lines passing thru C(h,k), with slopes m = ± b/a
Standard Form of an Equation of an Hyperbola opening up and down is:
 with C(h,k) and vertices 'b' units up and down from center
Foci units units up and down from center, along x = h
& Asymptote Lines passing thru C(h,k), with slopes m = ± b/a
the vertex form of a Parabola opening up(a>0) or down(a<0),  where(h,k) is the vertex.
The standard form is  , where the focus is (h,k + p)
the vertex form of a Parabola opening right(a>0) or left(a<0),  where(h,k) is the vertex.
The standard form is  , where the focus is (h +p,k )
Answer by math-vortex(648)  (Show Source):
You can put this solution on YOUR website!
Hi, there--
The Problem:
What are the vertices of the ellipse given by the equation x2 + 4y2 + 10x – 56y + 205 = 0?
A Solution:
By using the complete the square method, we will put this equation into this form:
Then we can easily see find the coordinates of the focal points.
x^2 + 4y^2 + 10x – 56y + 205 = 0
Subtract 205 from both sides of the equation.
x^2 +4y^2 + 10x -56y = -205
Rearrange the terms on the left hand side to gather all x-terms, then all y-terms.
(x^2 + 10x) + (4y^2-56y) = -205
Factor a 4 out of the y terms so the the coefficient of the y-squared term will be 1.
(x^2 + 10x) + 4(y^2-14y) = -205
We need to add a constant term to (x^2 +10x) that will give us a perfect square polynomial. To
find that constant, take half the coefficient of 10x and square it; half of 10 is 5, and 5-squared is
25.
We will add 25 to both sides of the equation.
(x^2 + 10x + 25) + 4(y^2 - 14y) = -205 + 25
Now we need to add a value to (y^2-14x) that will give us a perfect square polynomial. To find
the number, take half the coefficient of -14y and square it. So half of -14 is -7 and -7 squared
is 49.
We will add 49 inside the parentheses on the left side of the equation. On the right side of the
equation we need to add 4*49 since every term inside those parentheses is multiplied by 4.
(x^2 + 10x + 25) + 4(y^2 -14y + 49) = -205 + 25 + 4*49
Simplify the right hand side of the equation.
(x^2 + 10x + 25) + (4y^2 -56y + ) = -205 + 25 + 4*49
Since we now have two square polynomials, we can write them in factored form.
(x+ 5)^2 + 4(y-7)^2 = 16
.
Finally divide both sides of the equation by 16.
We can reduce 4/16 to 1/4 and 16/16 to 1.
Represent the denominators as squares.
After ALL this work, we have the equation in the form we want.
The center of the ellipse is the point (h,k) = (-5,7)
The value of a is 4 and the value of b is 2.
The vertices are located at (h+a,k) and (h-a,k). In this equation, we have the two vertices at
(-5+4,-7)=(-1,7) and (-5-4,7)=(-9,7)
The co-verticies are located at (h, k+b) and (h,k-b). In this equation, the co-verticies are located at
(-5,7+2)=(-5,9) and (-5,7-2)=(-5,5)
There is a lot of algebra here. Feel free to email me if you have questions about any of the solution.
Ms.Figgy
math.in.the.vortex@gmail.com
|
|
|
| |
