|
Question 621020: y^2-x^2/15=1
Want to know the focus,vertices and the asymptote
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! For hyperbolas, we like the standard form of the equation, the one that shows a difference of squares equal to 1.
It may look like
 or or  . .
That form of the equation shows you all the numbers you need to know to figure out the he foci, vertices and the asymptotes. (All you need is the a and b numbers).
 is the equation (in standard form) of a hyperbola centered at the origin, so this is an easy problem. is the equation (in standard form) of a hyperbola centered at the origin, so this is an easy problem.
We know this one is centered at the origin because there is just an  and a and a  , with nothing added or subtracted before squaring. , with nothing added or subtracted before squaring.
Because of that simplicity, it is easy to see that changing x to -x gives you the same equation, meaning that the graph is symmetrical with respect to the y-axis. The same can be said of changing y to -y, and the symmetry with respect to the x-axis.
For y=0 we would have a negative number equal to 1  and that cannot be. and that cannot be.
So, we can see that the graph does not touch the x-axis, where y=0. (In fact the graph does not even want to get close to the x-axis)
On the other hand, y cannot be zero, but x can be zero.
When  , you see that , you see that  , meaning , meaning  or or  , so the graph goes through the points (0,1) and (0,-1). , so the graph goes through the points (0,1) and (0,-1).
For all other points, 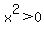 so so 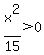 and and  , meaning that all the other points are even farther away from the x-axis, where y=0. , meaning that all the other points are even farther away from the x-axis, where y=0.
The closest that the hyperbola comes to the x-axis is the points (0,1) and (0,-1) , which are the vertices.
As x (and y) grow larger in absolute value,  and and  grow larger, and the graph gets closer to the asymptotes. grow larger, and the graph gets closer to the asymptotes.
A little algebra transforms the equation into one that gives us the equations of the asymptotes:
 --> -->  --> -->  --> -->  --> --> 
As  grows larger, grows larger, 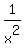 grows smaller, and the graph gets closer to the graph for grows smaller, and the graph gets closer to the graph for
 which is the graph for the lines which is the graph for the lines
 <--> <-->  and and
 <--> <-->  . .
Those lines are the asymptotes.
Because teachers do not like to see square roots in denominators, we may have to write them as
 and and  . .
THE FOCI:
There foci are at a distance  from the center of the hyperbola, and the number from the center of the hyperbola, and the number  is related to the numbers is related to the numbers  and and  in the standard form of the equation by a formula that can be derived using the Pythagorean theorem. It is in the standard form of the equation by a formula that can be derived using the Pythagorean theorem. It is

In this case, your  and and  are 1 and 15, so are 1 and 15, so
 --> -->  --> -->  . .
The center was (0,0) (the origin).
The vertices were ((0,-1) and (0,1), on the y-axis.
The foci are on the same line, but at distance 4 from the center/origin, at
(0,-4) and (0,4).
|
|
|
| |