SOLUTION: I need help trying to find the foci, center, and asymptote for this equations: {{{ -9x^2 + 25y^2 + 50y -200 = 0 }}}

 

Hi, 

 OR 

See below for details on an Hyperbola opening Up and Down:

See below descriptions of various conics                         

Standard Form of an Equation of a Circle is  

where Pt(h,k) is the center and r is the radius



 Standard Form of an Equation of an Ellipse is  where Pt(h,k) is the center. (a positioned to correspond with major axis)

 a and b  are the respective vertices distances from center and ±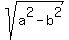are the foci distances from center: a > b



Standard Form of an Equation of an Hyperbola opening right and  left is:

   where Pt(h,k) is a center  with vertices 'a' units right and left of center.



Standard Form of an Equation of an Hyperbola opening up and down is:

   where Pt(h,k) is a center  with vertices 'b' units up and down from center.



the vertex form of a parabola opening up or down,  where(h,k) is the vertex.

The standard form is , where  the focus is (h,k + p)



the vertex form of a parabola opening right or left,  where(h,k) is the vertex.

The standard form is , where  the focus is (h +p,k )