Question 606915: Find the vertex, focus, directrix, and Axis of symetry for: x^2+10x+4y+9=0
I do not know what to do. :( I have been able to bring it to (x+5)^2 +4y =-9, but because there is no Y^2, I don't know what to do. :(
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
Yes, there is no y^2. This is a Parabola.
the vertex form of a parabola opening up or down,  where(h,k) is the vertex. where(h,k) is the vertex.
x^2+10x+4y+9=0
(x+5)^2 -25 + 4y + 9=0
(x+5)^2 + 4y -16 =0
 a = -1/4<0, open downwards, Center(-5,4) Axis of symmetry x=-5 a = -1/4<0, open downwards, Center(-5,4) Axis of symmetry x=-5
The standard form is  , where the focus is (h,k + p) , where the focus is (h,k + p)
4p = -4, p = -1 , focus is (-5,3) and directrix is y = 5

See below descriptions of various conics
Standard Form of an Equation of a Circle is 
where Pt(h,k) is the center and r is the radius
Standard Form of an Equation of an Ellipse is  where Pt(h,k) is the center. where Pt(h,k) is the center.
a and b are the respective vertices distances from center and ±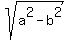 are the foci distances from center are the foci distances from center
Standard Form of an Equation of an Hyperbola opening right and left is:
 where Pt(h,k) is a center with vertices 'a' units right and left of center. where Pt(h,k) is a center with vertices 'a' units right and left of center.
Standard Form of an Equation of an Hyperbola opening up and down is:
 where Pt(h,k) is a center with vertices 'b' units up and down from center. where Pt(h,k) is a center with vertices 'b' units up and down from center.
the vertex form of a parabola opening up or down,  where(h,k) is the vertex. where(h,k) is the vertex.
The standard form is  , where the focus is (h,k + p) , where the focus is (h,k + p)
the vertex form of a parabola opening right or left,  where(h,k) is the vertex. where(h,k) is the vertex.
The standard form is  , where the focus is (h +p,k ) , where the focus is (h +p,k )
|
|
|