|
Question 583917: How do you convert the equation 4x^2+25y^2-24x+100y+36=0 to its standard form by completing the square on x and y. Then graph the ellipse and give the location of its foci.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Make a group with the x's and a group with the y's, to get

We need to subtract that loose constant number from both sides. At this point (rather than later), I also like to take out as common factors the coefficients of the squares. (See notes below for an alternative). When I do all that, I get:
 --> --> 
Now, you need to see those brackets and incomplete squares. For each bracket, think of a square (of a binomial) that equal what's in the bracket plus a number.
I immediately think of
 and and 
I verify the multiplication to make sure I got it right.
If you cannot "see" what the "completed square" would be, I'll list a trick below.
Next, you need to add the right numbers into those brackets to complete the squares, and at the same time you have to change the other side of the equal sign so as to make the equation equivalent.
We need an extra +9 inside the first bracket, but because the whole bracket is multiplied by 4, we really need to add  . .
Similarly, we need an extra +4 in the second bracket, but we need to add  . .
To have an equivalent equation, those amounts are added to both sides of the equation to get

Now we simplify, and get
 , ,
and then we write the completed squares as squares

Finally, we divide both sides of the equation by the number on the right of the equal sign, and simplify
 --> -->  , or , or
 , ,
NOTES AND TRICKS (optional reading):
At the beginning I could have kept the common factors in as

and the squares to be completed would be less easy to see, but I could use the fact that an expression like  can be completed to a square that is can be completed to a square that is
 . (If there's nothing in front of . (If there's nothing in front of  , then a=1 and it's just , then a=1 and it's just 
Anyway, for  and and  , the completed squares are , the completed squares are
 and and  . .
So, I would end up adding 36 and 100 to both sides of

to get  --> --> 
At the point I would really want to take out those common factors, to get

and dividing by 100, I would get
 or or  , anyway. , anyway.
GRAPHING:
The coordinates of the center of the ellipse are subtracted from x and y in those brackets. The ellipse is centered at (3,-2), the point with x=3, and y=-2.
In high school you should only get ellipses with horizontal and vertical axes (no term in xy).
The axes of your ellipse are the horizontal and vertical lines through the center of the ellipse, and and  respectively. respectively.
The ellipse extends to the right and left of the center and the vertical axis up to 5 units away because of the  dividing the bracket with the x. That length, 5, is called the semi-major axis. dividing the bracket with the x. That length, 5, is called the semi-major axis.
The ellipse extends above and below the center and horizontal axis up to 2 units away because of the 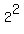 dividing the bracket with the y. That smaller length, 2, is called the semi-minor axis. dividing the bracket with the y. That smaller length, 2, is called the semi-minor axis.
We plot the center, the axes, and the points where the ellipse crosses the axes:

At this point, I would just draw something that looks like an ellipse and contains those 4 points where the ellipse crosses its axes.
You could calculate and plot other points, but that is more work than you should be required.
NOTE/EXPLANATION (optional reading):
When the ellipse crosses one of the axes, one of the brackets in the equation is zero, and what's left of the equation tells you that the point is as far away from the center as the number that's squared in the denominator.
At the horizontal axis  , ,  , and , and  . .
So,  , and , and  . .
That means that the ellipse crosses horizontal axis  5 units away (to the left and right) of the center (3,-2). 5 units away (to the left and right) of the center (3,-2).
Similarly for the vertical axis  , when x=3, , when x=3,  , ,  , and , and  . .
So the ellipse crosses the vertical axis 2 units above and below its center.
FOCI:
The foci are at a distance c from the center on the longer (major) axis, so they will be at (3-c,-2) and (3+c,-2).
The focal distance can be calculated from the length of the semi-major axis, a, and the length of the semi-minor axis, b, from the equation

In yout case b=2, a=5,  --> -->  --> -->  --> -->  is the focal distance. is the focal distance.
The foci are at (3- , -2) and (3+ , -2) and (3+ , -2) , -2)
NOTE/EXPLANATION (optional reading):
The equation  relating the focal distance with the semi-major axis and semi-minor axis derives from a right triangle, applying Pythagoras. The right triangle (shown below) has as vertices, the center of the ellipse, one co-vertex of the ellipse, and one of the foci. relating the focal distance with the semi-major axis and semi-minor axis derives from a right triangle, applying Pythagoras. The right triangle (shown below) has as vertices, the center of the ellipse, one co-vertex of the ellipse, and one of the foci.
 The vertex shown is at distances a+c and a-c from the foci. The sum of those distances is 2a. The vertex shown is at distances a+c and a-c from the foci. The sum of those distances is 2a.
The co-vertex is at the same distance from both foci. That distance is the length of the hypotenuse. The sum of its distances to the foci is twice the length of the hypotenuse.
By definition of ellipse, the sum of the distances to the foci is the same for all points of the ellipse.
So twice the length of the hypotenuse is 2a, and the length of the hypotenuse is a.
|
|
|
| |