Question 391376: A hyperbola has vertices (8,0)and (-8,0)Its foci are located at (√(89),0) and(-√(89),0) identify the equation of this hyperbola. I honestly have no Idea how to solve this please help.Thanks in advance. :)
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
vertices on the x-axis: (8,0)and (-8,0) Hyperbola opens right and left.
Standard Form of an Equation of an Hyperbola is 
where Pt(h,k) is a center with vertices 'a' units right and left of center
and asymptotes that pass thru the center with slope = ± b/a
In this example: center is (0,0) with a = 8
x^2/8^2 - y^2/b^2 = 1
foci (c,0) and (-c,0) are (sqrt(89), 0),-sqrt(89), 0 }}}
c, the distance from the center to the foci
c^ = a^2 + b^2
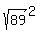 = 8^2 + b^2 = 8^2 + b^2
89 = 64 + b^2
25 = b^2
b = ± 5
x^2/8^2 - y^2/5^2 = 1


|
|
|