In your equation, the major axis is horizontal and the minor axis is vertical.
The foci are at (0,-4) and (0,4).
The center of the ellipse is at the point (0,0).
c is the distance between each focus and the center of the ellipse.
This means that c = +/- 4.
This means that c^2 = 16
The major axis of the ellipse is equal to 2a.
This means that a is the distance from the center of the ellipse to the intersection of the major axis of the ellipse with the ellipse.
The minor axis of the ellipse is equal to 2b.
This means that b is the distance from the center of the ellipse to the intersection of the minor axis of the ellipse with the ellipse.
the major axis of this ellipse is vertical.
the minor axis of this ellipse is horizontal.
A diagram of the major axis of this ellipse and the minor axis of this ellipse and the location of the foci and the intersection of the major and minor axis of this ellipse with the ellipse is shown below.
everything is drawn except the ellipse itself which I can't do.
P(major)
x
F2
b x
| x
| x
(minor)P x x x C x x x P(minor)
x x
a ----- x x ----- c
x x
F1
x
P(major)
In the diagram above:
P(minor) is the intersection of the minor axis with the ellipse.
P(major) is the intersection of the major axis with the ellipse.
F1 is the focal point at (0,-4).
F2 is the focal point at (0,4).
C is the center of the ellipse at (0,0).
c is the straight line distance between C and F1.
a is the straight line distance between F1 and P(minor) on the left of the diagram (line not shown).
b is the straight line distance between C and P(minor) on the left of the diagram.
This forms a right triangle with the points of the triangle being F1, C, and P(minor) on the left of the diagram.
By the Pythagorean formula, a^2 = b^2 + c^2.
This formula leads to c^2 = a^2 - b^2.
Since c^2 = a^2 - b^2, and since c = 4, this means that:
16 = a^2 - b^2
The problem states that the sum of the focal radii = 10.
The sum of the focal radii is a constant and is equal to the distance between F1 and a point on the ellipse plus the distance between F2 and the same point on the ellipse.
By definition, the sum of these distances is equal to 2a which is the diameter of the major axis.
Since 10 is equal to 2a, this means that a = 5 which is the length from the center of the ellipse to the perimeter of the ellipse along the major axis.
In the diagram, that would be from C to P(major) on the top of the diagram.
In the diagram, it is also from C to P(major) on the bottom of the diagram.
Since we know that a = 5, and we know that c = 4, we can derive b using the formula:
c^2 = a^2 - b^2
This becomes
4^2 = 5^2 - b^2 which becomes:
16 = 25 - b^2.
We solve for b to get b = sqrt(9) = 3.
b is the length from the center of the ellipse to the ellipse along the minor axis.
In the diagram, that would be from C to P(minor) on the left of the diagram.
In the diagram, that would also be from C to P(minor) on the right side of the diagram.
We now have:
a = 5
b = 3
c = 4
From this, we should be able to derive the formula for the ellipse.
The standard formula for an ellipse is:
(x-h)^2 / b^2 + (y-k)^2 / a^2 = 1
Since the two foci are at (0,-4) and at (0,4), this means that the vertex of the ellipse (otherwise known as the center of the ellipse) is at (0,0).
This means that (h,k) = (0,0), because (h,k) represent the center of the ellipse (otherwise known as the vertex of the ellipse).
Since h is zero, then (x-h)^2 becomes x^2.
since k is zero, then (y-k)^2 becomes y^2.
Our formula becomes:
x^2 / b^2 + y^2 / a^2 = 1
Since a = 5 and b = 3, this formula becomes:
x^2 / 3^2 + y^2 / 5^2 = 1 which becomes:
x^2 / 9 + y^2 / 25 = 1
To graph this equation, we have to solve for y as follows:
Equation is:
x^2 / 9 + y^2 / 25 = 1
Subtract x^2 / 9 from both sides of the equation to get:
y^2 / 25 = -x^2/9 + 1
Multiply both sides of the equation by 25 to get:
y^2 = (-25/9)x^2 + 25
Take the square root of both sides of the equation to get:
y = +/- sqrt((-25/9)x^2 + 25)
This makes y = sqrt((-25/9)x^2 + 25) and y = -sqrt((-25/9)x^2 + 25)
Graph of this equation looks like this:
In this graph, the foci are at (x,y) = (0,-4) and at (x,y) = (0,4).
The major axis is vertical at y = 0.
The minor axis is horizontal at x = 0.
The vertex is at (x,y) = (0,0).
The distance from the foci to the vertex is +/- 4 along the y-axis.
The sum of the focal radii will always be 10.
The answer to your question is that the equation for this ellipse is:
x^2/9 + y^2/25 = 1
The general form of that equation is:
x^2/b^2 + y^2/a^2 = 1
A picture of this ellipse is shown below:
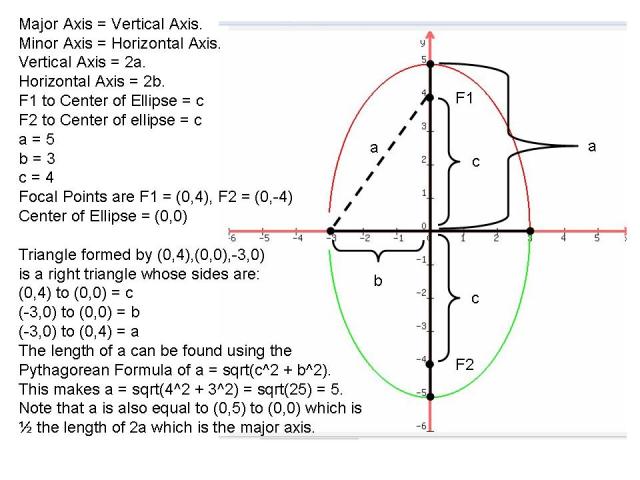
In this picture:
2a is the length of the major axis.
The designation for the distance from the surface of the ellipse to the center of the ellipse along the major axis is called "a".
2b is the length of the minor axis.
The designation for the distance from the surface of the ellipse to the center of the ellipse along the minor axis is called "b".
The designation for the distance from each focal point to the center of the ellipse is called "c".
F1 and F2 are the focal points of the ellipse.
The center of this ellipse is (0,0).
F1 is at (0,4) and F2 is at (0,-4).
*****
a also happens to be the hypotenuse of the right triangle formed by b and c as shown in the diagram. This is why the formula a^2 = b^2 + c^2 is valid.
Since a^2 = c^2 + b^2 is a valid equation (Pythagorean Formula for Right Triangle), the other formula that can be derived from this is:
c^2 = b^2 - a^2.
*****
What is not shown in this picture is the focal radii.
That will be shown in a separate picture below:
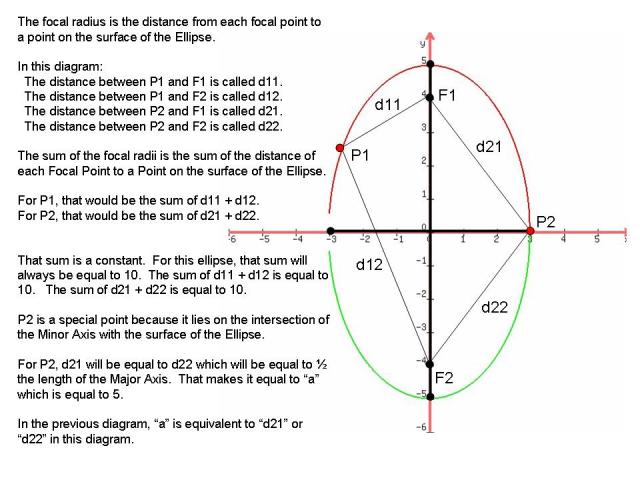
In this picture:
P1 is a point on the surface of the ellipse.
P2 is a point on the surface of the ellipse.
d11 is the distance from P1 to F1.
d12 is the distance from P1 to F2.
d21 is the distance from P2 to F1.
d22 is the distance from P2 to F2.
The focal radii shown on this ellipse are d11, d12, d21, d22.
From P1, the Sum of the focal radii are d11 and d12.
From P2, the Sum of the focal radii are d21 and d22.
The Sum of the focal radii is a contant.
This means that the sum will always be the same, regardless of which point on the surface of the ellipse you are at.
The Sum of d11 and d12 is equal to 10 for this ellipse.
The Sum of d21 and d22 is also equal to 10 for this ellipse.
A fairly decent reference regarding this problem can be found at the following website.
http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_conics_ellipse.xml