|
Question 1200120: Given the line 𝑥 + 2𝑦 − 4 = 0 and circle 𝑥^2 + 𝑦^2 − 8𝑥 − 4 = 0, find the equations of the tangents to the circles which are perpendicular to the line. Sketch the graph.
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given the line 𝑥 + 2𝑦 − 4 = 0 and circle 𝑥^2 + 𝑦^2 − 8𝑥 − 4 = 0,
Find the equations of the tangents to the circles which are perpendicular to the line.
Sketch the graph.
~~~~~~~~~~~~~~~~~~~~~~~~
The given circle equation is
x^2 + y^2 - 8x - 4 = 0.
By completing the square, you reduce it to the standard form circle equation
(x-4)^2 + y^2 = 20.
So, the circle has the center at the point C= (4,0) and has the radius of  = 4.472 (rounded).
Notice that the circle intersects y-axis at the points y= +/-2. So, y-intercepts are the points A= (0,2) and B= (0,-2).
The given line x + 2y - 4 = 0 has the slope m= -0.5.
Notice that this line goes through the center C= (4,0) of the circle and through the point A= (0,2).
so point A is actually an intersection point of the given line and the circle.
Thus we discovered very important fact: the given line goes through the center of the given circle.
+-----------------------------------------------------------------------+
| It implies that the lines tangent to the circle and perpendicular |
| to the given line factually go through the intersection points |
| of the given line and the circle. |
+-----------------------------------------------------------------------+
Thus the desired lines have the slope = 4.472 (rounded).
Notice that the circle intersects y-axis at the points y= +/-2. So, y-intercepts are the points A= (0,2) and B= (0,-2).
The given line x + 2y - 4 = 0 has the slope m= -0.5.
Notice that this line goes through the center C= (4,0) of the circle and through the point A= (0,2).
so point A is actually an intersection point of the given line and the circle.
Thus we discovered very important fact: the given line goes through the center of the given circle.
+-----------------------------------------------------------------------+
| It implies that the lines tangent to the circle and perpendicular |
| to the given line factually go through the intersection points |
| of the given line and the circle. |
+-----------------------------------------------------------------------+
Thus the desired lines have the slope 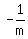 = = 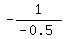 = 2, since they are perpendicular to the given line.
Next, one intersection point of the given line and the circle is the point A= (0,2).
Hence, the other intersection point of the given line and the circle is D= (8,-2),
symmetrical to A relative the center of the circle C= (4,0).
Thus first desired line has the slope 2 and goes through A= (0,2). Its equation is y-2 = 2x,
The second desired line has the slope 2 and goes through D= (8,-2). Its equation is y+2 = 2(x-8).
ANSWER. First desired line has equation y-2 = 2x.
Second desired line has equation y+2 = 2(x-8).
These equations can be presented in any other equivalent forms. = 2, since they are perpendicular to the given line.
Next, one intersection point of the given line and the circle is the point A= (0,2).
Hence, the other intersection point of the given line and the circle is D= (8,-2),
symmetrical to A relative the center of the circle C= (4,0).
Thus first desired line has the slope 2 and goes through A= (0,2). Its equation is y-2 = 2x,
The second desired line has the slope 2 and goes through D= (8,-2). Its equation is y+2 = 2(x-8).
ANSWER. First desired line has equation y-2 = 2x.
Second desired line has equation y+2 = 2(x-8).
These equations can be presented in any other equivalent forms.
Solved.
To make a sketch, go to web-site www.desmos.com/calculator and use free of charge plotting tool there.
Your job will be to print equations of the circle, of the given line and of the two desired lines.
|
|
|
| |