Question 1194067: The vertices of a hyperbola are the points (−3, 2) and (−3, −2) and the length of its conjugate is 6.
Find the equation of the hyperbola, the coordinates of its foci, and its eccentricity.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The vertices of a hyperbola are the points (−3, 2) and (−3, −2) and the length of its conjugate is 6.
Find the equation of the hyperbola, the coordinates of its foci, and its eccentricity.
~~~~~~~~~~~~~~~~~~~~~
From the given info, the center of the hyperbola is the point (-3,0)
and its real axis lies on vertical line x = -3.
Thus the hyperbola is "vertical", opened up and down.
Real semi-axis length is half the distance between the vertices a =  = =  = 2.
Also, from the given part, the length of its conjugate axis is 6; hence, conjugate semi-axis length is b = 6/2 = 3.
Now the standard form equation of the hyperbola is = 2.
Also, from the given part, the length of its conjugate axis is 6; hence, conjugate semi-axis length is b = 6/2 = 3.
Now the standard form equation of the hyperbola is
 - -  = 1. ANSWER
P L O T = 1. ANSWER
P L O T
 Hyperbola
Hyperbola  - -  = 1
In the plot, we can not see the imaginary axis and imaginary semi-axes: they are invisible.
But we can show the foci. They are ( = 1
In the plot, we can not see the imaginary axis and imaginary semi-axes: they are invisible.
But we can show the foci. They are ( , , ) and ( ) and ( , , ), where 13 = ), where 13 =  + +  = = 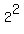 + +  . .
Solved.
|
|
|