|
Question 1184546: A radio telescope has a parabolic dish with a diameter of 110 meters. The
collected radio signals are reflected to one connection point, called the focal point, being the focus of the parabola. If the focal length is 50 meters, find the depth of the dish, rounded to two decimal places.
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
A radio telescope has a parabolic dish with a diameter of 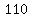 meters. The collected radio signals are reflected to one collection point, called the focal point, being the focus of the parabola.
If the focal length is  meters, find the depth of the dish, rounded to one decimal place.
To simplify my computations, I'll put the vertex of my parabola (that is, the base of the dish) at the origin, so ( ,  ) = ( , ).
Since the focal length is , then  and the equation is:
This parabola extends forever in either direction, but I only care about the part of the curve that models the dish. Since the dish has a diameter of a 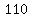meters, then I only care about the part of the curve from  to  .
The height of the edge of the dish (and thus the depth of the dish) will be the y-value of the equation at the "ends" of the modelling curve. The height of the parabola will be the same at either x-value, since they're each the same distance from the  , so it doesn't matter which value I use. I prefer positive values, so I'll plug  into my modelling equation:
 or about  meters
|
|
|
| |
