Question 1170467: The foci of an ellipse are (-3,-6) and (-3,2). For any point on the ellipse, the
sum of its distances from the foci is 14. Find the standard equation of the
ellipse.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From the condition, the major semi-axis is vertical and the distance between the foci is 2 - (-6) = 8.
Therefore, the eccentricity "e" is half of this distance, i.e. e = 8/2 = 4.
Let the foci be the points F1 and F2, and let V be the vertex of the ellipse closest to F1.
Then the distance from F1 to V is (a-e), while the distance from F2 to V is (a+e), where "a" is the major semi-axis.
The sum of these distances is equal to 14, according to the condition
(a-e) + (a+e) = 14,
which implies
2a = 14, a = 7.
Thus the major semi-axis is a = 7 and the eccentricity is 4.
Then from c = 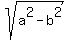 , we have for the minor semi-axis "b" , we have for the minor semi-axis "b"
 = = 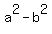 , ,
 = =  = =  = 49 - 16 = 33.
The center of the ellipse is at (-3,-2); therefore, its equation is = 49 - 16 = 33.
The center of the ellipse is at (-3,-2); therefore, its equation is
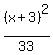 + +  = 1. = 1.
Solved.
|
|
|