SOLUTION: the endpoints of major and minor axes of an ellipse are (1,1),(3,4),(1,7)and(-1,4).sketch the ellipse give the question in standard form and find its foci eccentricity and directri

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: the endpoints of major and minor axes of an ellipse are (1,1),(3,4),(1,7)and(-1,4).sketch the ellipse give the question in standard form and find its foci eccentricity and directri      Log On


   

Question 1168162: the endpoints of major and minor axes of an ellipse are (1,1),(3,4),(1,7)and(-1,4).sketch the ellipse give the question in standard form and find its foci eccentricity and directrices
Found 2 solutions by solver91311, MathLover1:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


Sorry, I don't know how to put a question in standard form. But I can teach you this one lesson: Proofread your posts BEFORE you click 'Send'.


John

My calculator said it, I believe it, that settles it


I > Ø

Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
so, the endpoints of major axes are 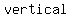(1,1) and (1,7), -> it’s ellipse with vertical major axis
distance 2b=6+=>b=3
the endpoints of minor axes are (3,4) and (-1,4), distance 2a=4+=>a=2
center is midpoint of both axes, at (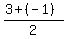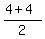%283%2B%28-1%29%29%2F2,%284%2B4%29%2F2)=(1,4+)=>+h=1, k=4


Standard form of equation for ellipse with vertical major axis:

%28x-h%29%5E2%2Fa%5E2%2B%28y-k%29%5E2%2Fb%5E2=1,
if
a=2
b=3
h=1
k=4
then
%28x-1%29%5E2%2F4%2B%28y-4%29%5E2%2F9=1

sketch the ellipse



give the question in standard form and find its foci eccentricity and directrices


Foci:
For an ellipse with major axis parallel to the y-axis, the foci points are defined as :
(h,+k%2Bc),(h,k-c), where c=sqrt%28b%5E2-a%5E2%29 is the distance from the center (h,k)
so, since h=1 and k=4 we have:
(1,4%2Bc),(1,4-c)
since a=2 and b=3, we have:
c=sqrt%28b%5E2-a%5E2%29=sqrt%283%5E2-2%5E2%29=sqrt%289-4%29=sqrt%285%29
then
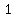(1,4-sqrt%285%29)≈(1,1.8}}}), (1,4%2Bsqrt%285%29)≈(1%2C6.2)
eccentricity is c%2Fb=sqrt%285%29%2F3
directrices: solve equation for y
y+=+%281%2F2%29%288-3sqrt%28-x%5E2%2B2x%2B3%29%29
y+=+%281%2F2%29%283sqrt%28-x%5E2%2B2x%2B3%29+%2B+8%29