SOLUTION: Find the value/s of U so that the graph of the equation of Ux^2 + y^2 − 2Ux = 0 is a hyperbola. Afterwards, identify the distance/s between the foci.

That will be the equation of a hyperbola if you pick any negative number
for U.  The easiest negative number to pick for U is -1:









Write y² as (y-0)² and factor out a negative from the two terms in x:



Complete the square by adding +1 inside the parentheses, which
amounts to adding -1 to the left side, so add -1 to the right
side also:



We write the second parentheses as the square of a binomial:



Since the right side is negative, we multiply through by -1



We reverse the terms on the left:



We put 1's under the two terms on the left:






We compare 

 to



The center is (h,k) = (1,0), a=1, b=1,

We calculate c, the distance fro center to foci from 







So the foci are  and ,

so the distance between the foci is



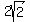If you chose any other negative number for U the answer would be different.

Edwin