|
Question 1149939: Write an equation for the given ellipse that satisfies the following conditions.
Center at (1,1); minor axis vertical, ,with length8; c=3
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Minor axis is 8 units --- hence, the minor semi-axis is b= 8/2 = 4 units.
Eccentricity c= 3 --- hence,
c^2 = a^2 - b^2 ===> a^2 = c^2 + b^2 = 3^2 + 4^2 = 25 ===> a =  = 5, where "a" is the major semi-axis.
Since minor axis is vertical, the ellipse "is wider than tall" and "a" goes with x-term, while "b" goes with y-terms.
Taking into account the center's position, the standard form equation of ellipse is = 5, where "a" is the major semi-axis.
Since minor axis is vertical, the ellipse "is wider than tall" and "a" goes with x-term, while "b" goes with y-terms.
Taking into account the center's position, the standard form equation of ellipse is
 + + 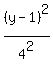 = 1. ANSWER = 1. ANSWER
Solved.
-----------------
For associated lessons, see
- Ellipse definition, canonical equation, characteristic points and elements
- Standard equation of an ellipse
- Identify elements of an ellipse given by its standard equation
- Find the standard equation of an ellipse given by its elements
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Conic sections: Ellipses. Definition, major elements and properties. Solved problems".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|
| |