|
Question 1136776: Hello! If someone could please help me solve this equation, I would be very grateful.
Find an equation for the ellipse with vertices at (-3, 4) and (15, 4); focus at (13, 4)
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! an equation for the ellipse with vertices at ( , ,  ) and ( ) and ( , ,  ); focus at ( ); focus at ( , ,  ) )
The equation of an ellipse is :
 for a horizontally oriented ellipse and for a horizontally oriented ellipse and
 for a vertically oriented ellipse. for a vertically oriented ellipse.
( , , ) is the center and the distance ) is the center and the distance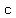 from the center to the foci is given by from the center to the foci is given by 
 is the distance from the center to the vertices and is the distance from the center to the vertices and  is the distance from the center to the co-vertices. is the distance from the center to the co-vertices.
The center of the ellipse is half way between the vertices.
so, ( , ,  ) => ( ) => ( , , ) )
Thus, the center ( , , ) of the ellipse is ( ) of the ellipse is ( , , ) and the ellipse is vertically oriented. ) and the ellipse is vertically oriented.
 is the distance between the center and the vertices, so is the distance between the center and the vertices, so 
 is the distance between the center and the foci, so is the distance between the center and the foci, so 




The equation is:


Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since you asked for help, that's exactly what I will do -- show you what you need to do to find the equation. Then, doing the work yourself, you will learn something from it.
The standard form of the equation of an ellipse with horizontal major axis centered at (h,k) is

In that formula, a is the semi-major axis (from the center of the ellipse to each end of the major axis) and b is the semi-minor axis (from the center to each end of the minor axis).
The two given vertices are the ends of the major axis; from that information you can determine the center of the ellipse (halfway between the two vertices) and the value of a (distance from the center to each vertex).
The only thing left you need to write the equation is the value of b.
The distance from the center of the ellipse to each focus is c, where a, b, and c are related by

Since you now know the center of the ellipse, the given coordinates of a focus allow you to determine the value of c; and from that you can determine the value of b.
Then you will have all you need to write the equation.
Good luck finishing.
If you need help finishing, post a "thank you" message indicating what progress you have made and where you need help.
|
|
|
| |