SOLUTION: Find a b and c of this ellipse 9x²-3y²-36x-6y+12=0

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find a b and c of this ellipse 9x²-3y²-36x-6y+12=0       Log On


   

Question 1125292: Find a b and c of this ellipse 9x²-3y²-36x-6y+12=0

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

                It is  NOT  AN  ELLIPSE  !     It is a hyperbola ! !

                Fix an error in your condition ! ! ! 


9x² - 3y² - 36x - 6y + 12 = 0.


Complete the squares for x-terms and y-terms separately, step by step


(9x^2 - 36x) - (3y^2 + 6y) = -12


9*(x^2 - 4x) - 3*(y^2 + 2y) = -12


9*(x^2 -4x + 4) - 3*(y^2 + 2y + 1) = -12 + 9*4 - 3


9*(x-2)^2 - 3*(y+1)^2 = 21.


Divide both sides by 21


%28x-2%29%5E2%2F%28%2821%2F9%29%29 - %28y%2B1%29%5E2%2F%28%2821%2F3%29%29 = 1,   or equivalently


%28x-2%29%5E2%2F%28%287%2F3%29%29 - %28y%2B1%29%5E2%2F7 = 1,


%28x-2%29%5E2%2F%28sqrt%287%2F3%29%29%5E2 - %28y%2B1%29%5E2%2F%28sqrt%287%29%29%5E2 = 1.    (Equation of a hyperbola)


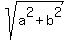Thus   a= sqrt%287%2F3%29,  b= sqrt%287%29,    and  c = sqrt%28a%5E2+%2B+b%5E2%29 = sqrt%287%2F3%2B7%29 = sqrt%2828%2F3%29 = 2%2Asqrt%287%2F3%29.