SOLUTION: For the hyperbola below, write the standard form equation. Then graph and tell the foci. Vertices: (8, 14) and (8, -10); conjugate axis is 6 units long

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: For the hyperbola below, write the standard form equation. Then graph and tell the foci. Vertices: (8, 14) and (8, -10); conjugate axis is 6 units long      Log On


   

Question 1116970: For the hyperbola below, write the standard form equation. Then graph and tell the foci.
Vertices: (8, 14) and (8, -10); conjugate axis is 6 units long
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The transverse axis, connecting the vertices is vertical, and has a length of
2a=14-%28-10%29%29=14%2B10=24 , so a=12 .
The conjugate axis has a length of
2b=6 , so b=3.
That makes the focal distance
c=sqrt%28a%5E2%2Bb%5E2%29=sqrt%2812%5E2%2B3%5E2%29=sqrt%28144%2B9%29=sqrt%28154%29 .
The center is the midpoint of the segment connecting the vertices,
so its coordinates are
h=8 and k=%2814%2B%28-10%29%29%2F2=2 .
Then, the coordinates of the foci are
x=8 (like the center and vertices), and
y=2%2Bsqrt%28154%29 and y=2%2Bsqrt%28154%29 .
highlight%28F%5B1%5D=8%2C2%2Bsqrt%28154%29%29 and highlight%28F%5B2%5D=8%2C2-sqrt%28154%29%29
Given the coordinates found for the center,
we know that the equation will involve
the squares of horizontal and vertical distances to the center:
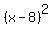%28x-8%29%5E2 and %28y-2%29%5E2 .
Obviously, as the vertices are a vertical distance a=12 from the center,
%28y-2%29%5E2%3E=12%5E2 <--> %28y-2%29%5E2%2F12%5E2%3E=1 ,
and the term %28y-2%29%5E2%2F12%5E2%3E=1 cannot be the one with the minus sign.
The equation is
highlight%28%28y-2%29%5E2%2F12%5E2-%28x-8%29%5E2%2F3%5E2=1%29 or highlight%28%28y-2%29%5E2%2F144-%28x-8%29%5E2%2F9=1%29 .

GRAPH:
The two arms of the hyperbola are drawn in green and red.
Asymptotes, transverse and conjugate axes are in blue.
The foci are the two black dots.
The foci are really close to the vertices,
but that is because the ratio of the lengths of transverse to conjugate axes is so large that c is just a hair longer than a .