|
Question 1042977:  x^2+y^2-2gx+2fy+e=0 has its center in the first quadrant. The x and y axes are tangents to C and x^2+y^2-2gx+2fy+e=0 has its center in the first quadrant. The x and y axes are tangents to C and
 the point (3,6) is on the circle. Find two equation of C. the point (3,6) is on the circle. Find two equation of C.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
 x^2+y^2-2gx+2fy+e=0 has its center in the first quadrant. The x and y axes are tangents to C and x^2+y^2-2gx+2fy+e=0 has its center in the first quadrant. The x and y axes are tangents to C and
 the point (3,6) is on the circle. Find two equations of C. the point (3,6) is on the circle. Find two equations of C.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
1. Since the axes x- and y- are tangents to C, the center of C lies on the line x = y. (which is the diagonal of the QI).
In other words, the center of the circle is at the point (x0,x0) for some x0 (now unknown).
2. Due to the same reason, the radius of the circle is equal to x0 (and to y0, too).
3. So, the equation of the circle is
 = =  . (1)
The point (3,6) lies on the circle, so coordinates satisfy the equation (1). In other words, . (1)
The point (3,6) lies on the circle, so coordinates satisfy the equation (1). In other words,
 = =  .
4. It gives you a quadratic equation for .
4. It gives you a quadratic equation for  . .
 = =  .
Simplify and solve for .
Simplify and solve for  : :
 = =  .
The roots are .
The roots are  = 5 and = 5 and  = 9.
5. The first circle has the center (5,5) and the radius 5.
Its equation is = 9.
5. The first circle has the center (5,5) and the radius 5.
Its equation is 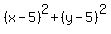 = 25.
The second circle has the center (9,9) and the radius 9.
Its equation is = 25.
The second circle has the center (9,9) and the radius 9.
Its equation is  = 81. = 81.
Solved.
|
|
|
| |