Question 1003743: How to convert the following equation into standard form and solve for the following:
付he location of the foci
付he coordinates of the of the center of the ellipses
2xｲ − 8x + 3yｲ + 12y = 6
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! 
WITHOUT MEMORIZED FORMULAS:
Looking at that last equation, we realize that
the curve is symmetrical
with respect to the line  <--> , and
with respect to the line  <--> .
We also realize that the curve it represents has
 <--> <--> <--> , and
 <--> <--> <--> .
Realizing all that, we figure that
it must be an ellipse, centered at point (2,-6), the point with  .
We also see that the vertices are
the point with  , and
the point with  ,
and we see that the co-vertices are
the point with  , and
the point with  .
  = semi-minor axis ,  = semi-major axis, and  = focal distance (which we need to find).
 and  are the foci, and for every point on the ellipse, the sum of distances to the foci is the same.
For point A, that sum is  ; for point D, it is  .
You can figure out that  , and since  ,
then  -->  ,
and applying the Pythagorean theorem to the right triangle ACF you get
 , or  or, with numbers,
 ---> ---> ---> .
So the location of focus F is (2,-6+5)=(2,-1) ,
and the location of focus G is (2,-6-5)=(2,-11)
WITH MEMORIZED FORMULAS:
The equations  and  with 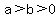 represents ellipses,
centered at point (h,k), whose semi-major axis is  and
and whose semi-minor is  ,
and the major axis is parallel to the coordinate axis corresponding to the variable in the square divided by  .
The focal distance  is found from .
is an equation of the form ,
so it represents an ellipse with major axis parallel to the y-axis,
with  ,
meaning that the center is at (2,-6).
Substituting into we get
--->---> .
That means that the foci are on a vertical line (parallel to the y-axis),  units above and below the center,
at (2,1) and 2,-11).
|
|
|
