SOLUTION: In an army navigation exercise, a group of soldiers hiked due south from base camp for 2.5 km to a water hole. From there, they turned 45� to the left, to head south-east for 1.6 k

Question 1109461: In an army navigation exercise, a group of soldiers hiked due south from base camp for 2.5 km to a water hole. From there, they turned 45� to the left, to head south-east for 1.6 km to a resting point. When the soldiers were at the resting point, how far (correct to one decimal place):
a) east were they from the water hole?
b) south were they from the water hole?
c) were they in a straight line from base camp?
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
point A is their base camp.

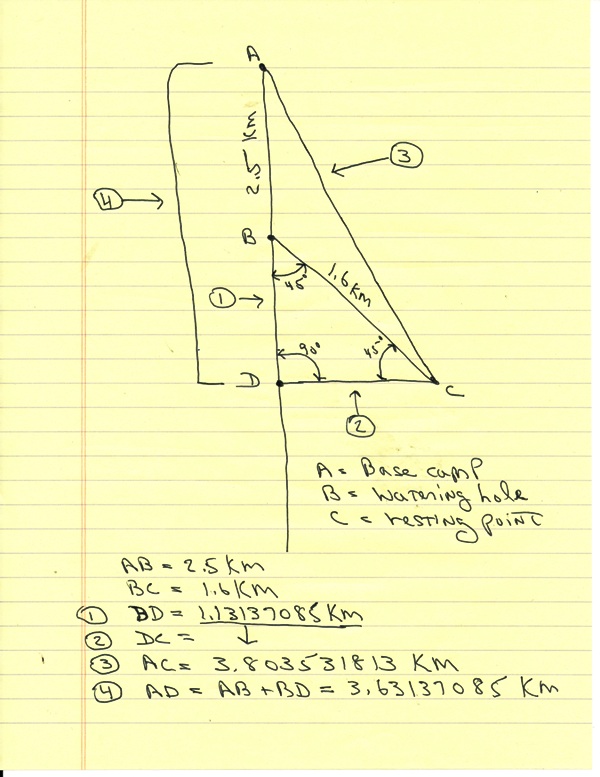
point B is the water hole which is 2.5 km directly south of point A.

point C is the rest point which is 1.6 km 45 degrees south east from point B.

point D is directly west from point C and directly south from point B.

points B, C, and D form right triangle BCD.

angles B and C in this triangle are each 45 degrees.

angle D is 90 degrees.

sin(B) = DC / BC.

this becomes sin(45) = DC / 1.6

solve for DC to get DC = 1.6 * sin(45) = 1.13137085 kilometers.

sin(C) = BD / BC.

this becomes sin(45) = BD / 1.6

solve for BD to get BD = 1.6 * sin(45) = 1.13137085 kilometers.

BD and DC are both 1.13137085 kilometers in length.

this makes right triangle BCD an isosceles right triangle.

the length of AD is the distance between the base camp and the point directly west of the rest point and directly south from the base camp.

this distance is 2.5 + 1.13137085 kilometers which is equal to 3.63137085 kilometers.

the points A, C, and D form right triangle ACD.

AD and DC are legs of this right triangle.

AC is the hypotenuse of this right triangle.

AC is also the straight line distance from point A to point C, which is the straight line distance from the base camp to the rest point.

by the pythogarus formula, [AD]^2 + [DC]^2 = [AC]^2

this makes [AC]^2 = to 3.63137085^2 + 1.13137085^2 = 14.46685425.

AC is equal to sqrt([AC]^2) which makes AC = 3.803531813 kilometers.

your questions are:

When the soldiers were at the rest point, how far (correct to one decimal place):
a) east were they from the water hole?
b) south were they from the water hole?
c) were they in a straight line from base camp?

answer to a):

they were 1.13137085 kilometers east of the water hole.
that would be the distance from point C to point D on the diagram.

answer to b):

they were 1.3137085 kilometers south of the water hole.
that would be the distance from point D to point B on the diagram.

answer to c):

they were 3.803531813 kilometers away from the base camp in a straight line from the base camp to the rest point.
that would be the distance form point A to point C on the diagram.

you should round your answer to the number of decimal places required.

here's the diagram:

$$$

RELATED QUESTIONS
Choose the most efficient strategy for solving the following problem: A group of... (answered by richwmiller)

How many soldiers are there in a group of 27 sailors and soldiers if there are four... (answered by josmiceli)

To deliver a message, an army officer will travel by car at 75mph from Camp A to Camp B,... (answered by ankor@dixie-net.com)

A group of students are bushwalking. They walk north from their camp for 7.5 km, then... (answered by Alan3354,Cromlix)

At a Forest Service Youth Camp, many of the workers ate some meals away from the base... (answered by stanbon)

How many soldiers are there in a group of 27 sailors and soldiers if there are four... (answered by ewatrrr)

An Army camp consists of 800 soldiers and their canteen has food provision that last for... (answered by ankor@dixie-net.com)

Susan hiked from her camp, going North for exactly 4 miles. Then she made a turn and... (answered by rfer,nerdybill)

Hilary and Dale leave camp and go for a long hike. After going 7 km due east, they turn... (answered by Alan3354)