Question 1062757: Find the length of a side of an equilateral triangle with a height of 5√3
Found 2 solutions by Theo, MathTherapy:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i think the length of the side is equal to 10.
here's why.
by pythagorus, the hypotenuse squared is equal to the sum of each leg squared.
your altitude is 5 * sqrt(3).
that's one of the legs of the right triangle formed.
let the hypotenuse of the right triangle be equal to b.
the other leg of the right triangle is equal to b/2.
that's because each leg of an the equilateral triangle is equal to b.
if you drop a perpenddicular from one of the vertices, it divided the opposite side into 2 equal parts.
two right triangles are formed.
we're working with one of the right triangles.
it has one leg equal to 5 * sqrt(3), one leg equal to b/2, and a hypotenuse equal to b.
by pythagorus, you get 5 * sqrt(3) + (b/2)^2 = b^2
simplify this to get 25 * 3 + b^2/4 = b^2
simplify further to get 75 + b^2/4 = b^2
subtract b^2/4 from both sides to get 75 = b^2 - b^2/4
multiply b^2 by 4/4 to get 75 = 4b^2/4 - b^2/4
combine like terms to get 75 = 3b^2/4
multiply both sides by 4 and divide both sides by 3 to get 75*4/3 = b^2
simplify to get 100 = b^2
solve for b to get b = 10.
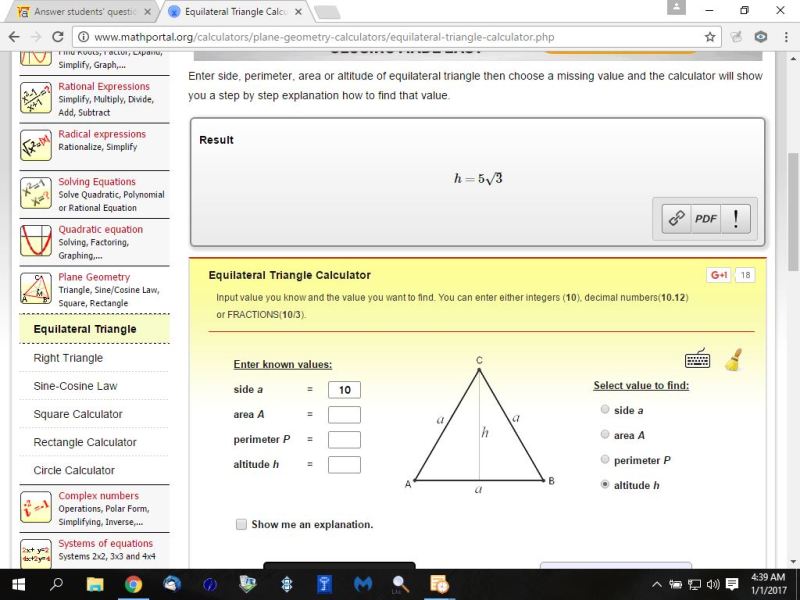
the results from this calculator confirm the solution is correct.
i entered a side length of 10 and it gave me the altitude of 5 * sqrt(3).
http://www.mathportal.org/calculators/plane-geometry-calculators/equilateral-triangle-calculator.php
here's a picture of the result.
Answer by MathTherapy(10579)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the length of a side of an equilateral triangle with a height of 5√3
The altitude of any equilateral triangle, drawn from any vertex to the 3rd side will BISECT the vertex it's drawn from, as well as the 3rd side it's drawn to.
Therefore, two (2) 30-60-90 right triangles are formed by this altitude. This also makes the altitude, the LONGER LEG, of each 30-60-90 triangle.
The hypotenuse (one of the equilateral triangle's sides) is calculated as: 
It's as easy as that....nothing COMPLEX and/or CONFUSING!
|
|
|