here's why.
by pythagorus, the hypotenuse squared is equal to the sum of each leg squared.
your altitude is 5 * sqrt(3).
that's one of the legs of the right triangle formed.
let the hypotenuse of the right triangle be equal to b.
the other leg of the right triangle is equal to b/2.
that's because each leg of an the equilateral triangle is equal to b.
if you drop a perpenddicular from one of the vertices, it divided the opposite side into 2 equal parts.
two right triangles are formed.
we're working with one of the right triangles.
it has one leg equal to 5 * sqrt(3), one leg equal to b/2, and a hypotenuse equal to b.
by pythagorus, you get 5 * sqrt(3) + (b/2)^2 = b^2
simplify this to get 25 * 3 + b^2/4 = b^2
simplify further to get 75 + b^2/4 = b^2
subtract b^2/4 from both sides to get 75 = b^2 - b^2/4
multiply b^2 by 4/4 to get 75 = 4b^2/4 - b^2/4
combine like terms to get 75 = 3b^2/4
multiply both sides by 4 and divide both sides by 3 to get 75*4/3 = b^2
simplify to get 100 = b^2
solve for b to get b = 10.
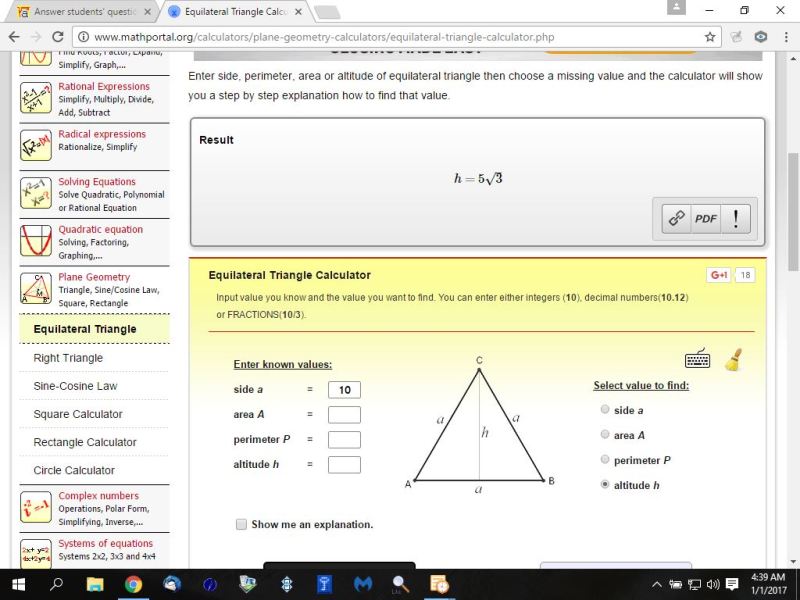
the results from this calculator confirm the solution is correct.
i entered a side length of 10 and it gave me the altitude of 5 * sqrt(3).
http://www.mathportal.org/calculators/plane-geometry-calculators/equilateral-triangle-calculator.php
here's a picture of the result.