SOLUTION: The sum of the squares of 6 consecutive integers is 1111. What are the integers? (once again, explain your reasoning).

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: The sum of the squares of 6 consecutive integers is 1111. What are the integers? (once again, explain your reasoning).       Log On


   

Question 163472: The sum of the squares of 6 consecutive integers is 1111. What are the integers? (once again, explain your reasoning).
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
Let's call the first integer, N.
the next 5 consecutive integers would be
N%2B1
N%2B2
N%2B3
N%2B4
N%2B5
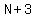
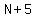
and their squares would be,
N%5E2=N%5E2
%28N%2B1%29%5E2=N%5E2%2B2N%2B1
%28N%2B2%29%5E2=N%5E2%2B4N%2B4
%28N%2B3%29%5E2=N%5E2%2B6N%2B9
%28N%2B4%29%5E2=N%5E2%2B8N%2B16
%28N%2B5%29%5E2=N%5E2%2B10N%2B25
Now add them together,


You know the sum of the squares equals 1111.
6N%5E2%2B30N%2B55=1111
6N%5E2%2B30N-1056=0
N%5E2%2B5N-176=0
%28N%2B16%29%28N-11%29=0
Two solutions.
.
.
.
N-11=0
N=11
The integers are then 11,12,13,14,15,16.
.
.
.
N%2B16=0
N=-16
The integers are then -16,-15,-14,-13,-12,-11.