3 cards are drawn from 12 face cards of ordinary deck of 52 playing cards. Let x be the number of kings and y be the number of jacks. Find the joint probability distribution of x and y.
J♥ Q♥ K♥
J♦ Q♦ K♦
J♠ Q♠ K♠
J♣ Q♣ K♣
The trinomial probability formula for non-negative integers x,y,z
where x+y+z = 3
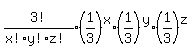 or
or 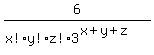 Let z = the number of queens (i.e., non-jacks, non-kings)
Substitution in that formula gives the following trinomial
distribution:
x y z p(x,y,z)
--------------------------------
0 0 3 1/27 = 0.03703704
0 1 2 3/27 = 0.11111111 = 1/9
0 2 1 3/27 = 0.11111111 = 1/9
0 3 0 1/27 = 0.03703703
1 0 2 3/27 = 0.11111111 = 1/9
1 1 1 6/27 = 0.22222222 = 2/9
1 2 0 3/27 = 0.11111111 = 1/9
2 0 1 3/27 = 0.11111111 = 1/9
2 1 0 3/27 = 0.11111111 = 1/9
3 0 0 1/27 = 0.03703703
Edwin
Let z = the number of queens (i.e., non-jacks, non-kings)
Substitution in that formula gives the following trinomial
distribution:
x y z p(x,y,z)
--------------------------------
0 0 3 1/27 = 0.03703704
0 1 2 3/27 = 0.11111111 = 1/9
0 2 1 3/27 = 0.11111111 = 1/9
0 3 0 1/27 = 0.03703703
1 0 2 3/27 = 0.11111111 = 1/9
1 1 1 6/27 = 0.22222222 = 2/9
1 2 0 3/27 = 0.11111111 = 1/9
2 0 1 3/27 = 0.11111111 = 1/9
2 1 0 3/27 = 0.11111111 = 1/9
3 0 0 1/27 = 0.03703703
Edwin