Question 333027: A random sample of tootsie rolls. The results in grams were: 3.087 3.131 3.241 3.241 3.270 3.353 3.400 3.411 3.437 3.477
A. Construct a 90% confidence interval for the true mean weight.
B. What sample size would be neccessary to estimate the true weight with an error of +0.03 grams with 90% confidence.
C. Discuss the factors which might cause variation in the weight of the tootsie rolls during manufacture.
Answer by jrfrunner(365)   (Show Source):
You can put this solution on YOUR website! Based on the given values:
average=3.305, standard dev =S =0.1320, sample size=10, 90% confidence interval for 
----
Since n is small, the population variance is unknown, analysis on the mean, it does not quite fit the requirements of a normal distribution, the Central limit theorem requires large sample sizes for analysing the averages. This cannot be done without assuming that the underlying distribution is Normal, otherwise you need to resort to non-parametric methods.
--
I'll assume you have normally distributed data (important assumption).
since n is small and population variance is unknown, this is a t distribution.
--
90% confidence interval for
find the critical values. t(critical) = t(tail pro=0.05, dof=9)=-/+1.833
compute standard error: 
--
use formulae: Xbar - t(critical)*SE, Xbar + t(critical)*SE
3.305-1.833*(0.0417), 3.305+1.833*(0.0417)
===
To determine sample size
Margin of Error = t(critical)*SE = t(critrical)*S/sqrt(n)
Solve for n: 
--
we know S=0.132, we are given ME=0.03, and 90% conf
n=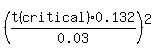 , but what value of t(critical)?????
some people subsitute the large normal sample critical value Z, which you can try, for 90% conf Z=1.645
--
The real method to use is an "iterative" where you try different values of t(critical) until the changes are minimal to none, but most people are unwilling to do this.
--
if you use Z=1.645
n= round up to 53
====
factors which might cause variation in the weight of the tootsie rolls during manufacture
--
in general, the factors affecting process relate to
*people: level of training, skill level, attention to details, motivation, etc
*machinery: Set up, age of machinery, malfunctions
*instruments: accuacy, precision, human error in readings
*enviroment: lighting, humidity, temperature
*Procedure: how well methods are established, documented, following them exactly,
|
|
|
