Statistics - 5 items in drawer (A,B,C,D,E). Choose 2 with replacement.
5 items in drawer (A,B,C,D,E). Choose 2 with replacement.
You have listed the wrong sample space! The sample space you
listed is the 5! or 120 ways or rearranging all the items in a row.
This is NOT what we are doing in this problem. What we are doing
is drawing one item, replacing it, and then drawing another.
Here is the sample space, where, for example (C,B) means that
C was drawn first then B was drawn second.
(A,A) (A,B) (A,C) (A,D) (A,E)
(B,A) (B,B) (B,C) (B,D) (B,E)
(C,A) (C,B) (C,C) (C,D) (C,E)
(D,A) (D,B) (D,C) (D,D) (D,E)
(E,A) (E,B) (E,C) (E,D) (E,E)
--------------------
P(same letter)
(A,A) (A,B) (A,C) (A,D) (A,E)
(B,A) (B,B) (B,C) (B,D) (B,E)
(C,A) (C,B) (C,C) (C,D) (C,E)
(D,A) (D,B) (D,C) (D,D) (D,E)
(E,A) (E,B) (E,C) (E,D) (E,E)
I've colored the ones with the same letter red.
So there are 5 out of 25 and the probability is 
--------------------
P(A and B)
(A,A) (A,B) (A,C) (A,D) (A,E)
(B,A) (B,B) (B,C) (B,D) (B,E)
(C,A) (C,B) (C,C) (C,D) (C,E)
(D,A) (D,B) (D,C) (D,D) (D,E)
(E,A) (E,B) (E,C) (E,D) (E,E)
I've colored the ones with both an A and a B red.
So there are 2 out of 25 and the probability is 
--------------------
P(A or B)
(A,A) (A,B) (A,C) (A,D) (A,E)
(B,A) (B,B) (B,C) (B,D) (B,E)
(C,A) (C,B) (C,C) (C,D) (C,E)
(D,A) (D,B) (D,C) (D,D) (D,E)
(E,A) (E,B) (E,C) (E,D) (E,E)
I've colored the ones with either an A or a B red.
So there are 16 out of 25 and the probability is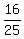 
---------------------
P(A and B|1st selection A)
(A,A) (A,B) (A,C) (A,D) (A,E)
(B,A) (B,B) (B,C) (B,D) (B,E)
(C,A) (C,B) (C,C) (C,D) (C,E)
(D,A) (D,B) (D,C) (D,D) (D,E)
(E,A) (E,B) (E,C) (E,D) (E,E)
Notice that since we are given that the 1st selection
was A, then we eliminate all the members of the sample
space except those that have the given condition, namely
that the first selection was A. Above I have lined through
all the ones that are eliminated by the given condition
that the first selection is A. That leaves only 5
members of the reduced sample space, and (A,B) is the
only successful one, so the probability is 
--------------------
P(A and B/1st selection not E)
(A,A) (A,B) (A,C) (A,D) (A,E)
(B,A) (B,B) (B,C) (B,D) (B,E)
(C,A) (C,B) (C,C) (C,D) (C,E)
(D,A) (D,B) (D,C) (D,D) (D,E)
(E,A) (E,B) (E,C) (E,D) (E,E)
Notice that since we are given that the 1st selection
was not E, then we eliminate all the members of the sample
space except those that have the given condition, namely
that the first selection was not E. Above I have lined through
all the ones that are eliminated by the given condition
that the first selection is not E. That leaves only 20
members of the reduced sample space, and (A,B) and (B,A) are
the only successful ones, so the probability is 
Edwin
