Question 1209507: Recall that there are 4 suits - spades, hearts, clubs, and diamonds - in a standard deck of playing cards. Suppose you play a game in which you draw a card, record the suit, replace it, shuffle, and repeat until you have observed 10 cards. Define X = numbers of spades observed.
Find the probability of observing 3 or fewer spades in this game. Round to three decimal places.
Found 3 solutions by mccravyedwin, ikleyn, math_tutor2020:
Answer by mccravyedwin(417)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Probability of getting a spade = 1/4
That's a cumulative binomial distribution problem
Got a TI-84?
2nd, vars, scroll to binomcdf enter
trials:10
p:1/4
x value:3
Paste
Scroll to Paste
enter
see binomcdf(10,1/4,3)
enter
0.7758750914 round to 0.776
Edwin
Answer by ikleyn(53339)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Recall that there are 4 suits - spades, hearts, clubs, and diamonds - in a standard deck
of playing cards. Suppose you play a game in which you draw a card, record the suit,
replace it, shuffle, and repeat until you have observed 10 cards. Define X = numbers of spades observed.
Find the probability of observing 3 or fewer spades in this game. Round to three decimal places.
~~~~~~~~~~~~~~~~~~~~~~~~~~
In this game, there are 4 suits, and every suit has the same number of card, 13,
so the total number of cards in a standard deck is 4*13 = 52.
At each step, this game returns us to the same initial condition, due to replacing and
shuffling the cards.
Therefore, this game is a typical binomial experiment. At each trial, we have a spade
with the probability 1/4 = 0.25 or any other suit card with the probability 3/4 = 0.75.
So, they want you calculate the probability of having success (having a spade) 3 or fever
times of 10 trials.
Use the standard formula for the binomial probability
P(X <= 3) = P(0) + P(1) + P(2) + P(3)
where P(k) = 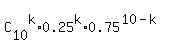 , , 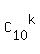 are binomial coefficients are binomial coefficients 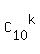 = = 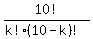 .
Now calculate using a calculator
P(0) = .
Now calculate using a calculator
P(0) = 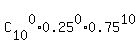 = = 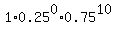 = 0.056313515;
P(1) = = 0.056313515;
P(1) =  = = 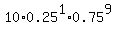 = 0.187711716;
P(2) = = 0.187711716;
P(2) = 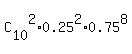 = = 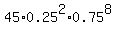 = 0.281567574;
P(3) = = 0.281567574;
P(3) = 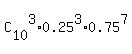 = =  = 0.250282288.
Finally, add the number and get
P(X <= 3) = 0.056313515 + 0.187711716 + 0.281567574 + 0.250282288 = 0.775875092.
Round it to 3 decimals. So, P(X <= 3) = 0.776 (rounded). ANSWER
You may check this result by using a convenient online binomial calculator at
https://stattrek.com/online-calculator/binomial.aspx = 0.250282288.
Finally, add the number and get
P(X <= 3) = 0.056313515 + 0.187711716 + 0.281567574 + 0.250282288 = 0.775875092.
Round it to 3 decimals. So, P(X <= 3) = 0.776 (rounded). ANSWER
You may check this result by using a convenient online binomial calculator at
https://stattrek.com/online-calculator/binomial.aspx
At this point, the problem is solved completely.
Answer by math_tutor2020(3827)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If your teacher lets you use a spreadsheet, then you can quickly find the answer using the BinomDist function.
The template is
=BinomDist(x,n,p,c)
x = number of successes
n = number of trials
p = probability of success
c = cumulative flag
In this case x = 3, n = 10, p = 1/4 = 0.25
c = 1 indicates that we're adding binomial probability values from x = 0 to x = 3
Therefore the full command to type in would be:
=BinomDist(3,10,0.25,1)
This leads to this approximate value 0.775875
which rounds to the final answer 0.776
Side note: Don't forget the equal sign up front of the BinomDist command.
|
|
|