SOLUTION: In a large population, about 45 % of people prefer tea over coffee. A researcher takes a random sample of 13 people and surveys whether they prefer tea over coffee.

Question 1207399: In a large population, about
45
%
of people prefer tea over coffee. A researcher takes a random sample of
13
people and surveys whether they prefer tea over coffee.
Use the binomial distribution to compute the probability that exactly
6
of the people in the sample prefer tea over coffee.
Identify the following information required to find the probability of people who prefer tea over coffee.
Provide your answer below:
n =
trials
x =
successes
p =
probability of those who prefer tea (as a decimal, not percent)

Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
the binomial probaiblity formula is p(x) = p^x * q^(n-x) * c(n,x)

p is the probability of occurrence which is equal to .45 in this problem.
q is the probability of no occurrence which is equal to 1 - p which is equal to .55 in this problem.
n is the sample size.

c(n,x) is the number of combinations of x occurrence from a pool of n occurrences.
that formula is equal to n! / (x! * (n-x)!).

probability of exactly 6 occurrences becomes p(6) = .45^6 * .55^7 * c(13,6) which is equal to .2169357825.

i used excel to calculate all the probabilities.
the sum of those probabilities must be equal to 1, as they are.

here are the results from the excel analysis.

Answer by ikleyn(52776) (Show Source): You can put this solution on YOUR website!
.
In a large population, about 45% of people prefer tea over coffee.
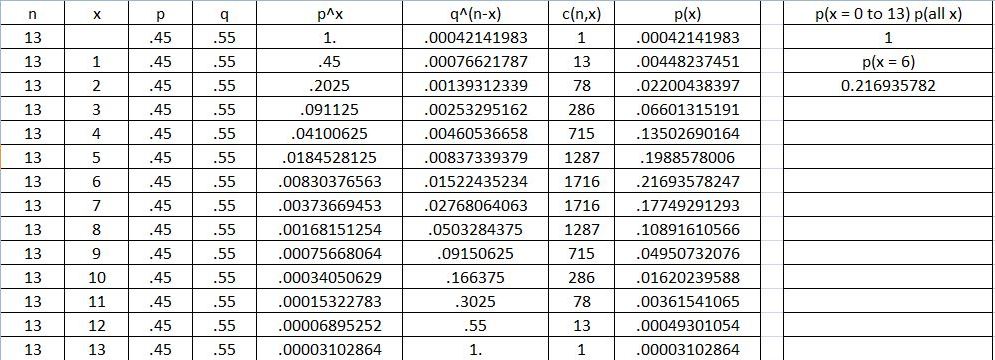
A researcher takes a random sample of 13 people and surveys whether they prefer tea over coffee.
Use the binomial distribution to compute the probability that exactly 6 of the people in the sample
prefer tea over coffee.
Identify the following information required to find the probability of people who prefer tea over coffee.
Provide your answer below:
n = trials; x = successes; p = probability of those who prefer tea (as a decimal, not percent)
~~~~~~~~~~~~~~~~~~~~~~~~~~~

People are independent in their preferences; the number of trials n is fixed (n = 13); there are only two possible outcomes in each trial, and the probability to get one of the two outcomes in each individual trial is a constant value (0.45 for tea over coffee). Thus we have a binomial distribution n = 13 (the number of trials); x = 0.45 is the probability of one of the two outcomes (tea) for each individual trial. They want you find the probability that of 13 people 6 will choose tea. Use the formula for this binomial probability P = = = 0.216935782. Rounded with 4 decimals after the decimal point, the ANSWER is 0.2169. Here 1716 = = is the binomial coefficient. You can calculate it using your calculator or using the standard function COMBIN(13,6) in Excel.

Solved.

There is no need to make calculations, writing or reasoning longer than that.

RELATED QUESTIONS
In a large population, about 45% of people prefer tea over coffee. A researcher takes a... (answered by ikleyn)
According to Statistics Canada (Share of Non-Alcoholic Beverage Market, 2008), 16% of... (answered by stanbon)
In a town every person takes at least one cup of coffee or tea. if 3/5th of the... (answered by flame8855)
45% people in a city like tea 30% like coffee and the remaining do not like any of the... (answered by ikleyn)
A researcher wishes to estimate the proportion of left-handers among a certain... (answered by Boreal)
At a breakfast buffet, 45% of people choose coffee for their beverage while 25% choose... (answered by Muchacho1994,MathTherapy)
Out of 50 people, 31 drink tea, 20 drink coffee, and 6 drink both tea AND coffee.... (answered by ikleyn)
A random sample of 1000 students showed 535 perfer coffee over tea. If the percentage of (answered by stanbon)
You read about a survey in a newspaper and find that 70% of the 250 people sampled prefer (answered by Boreal)