SOLUTION: The Acme Company manufactures widgets. The distribution of widget weights is bell-shaped. The widget weights have a mean of 56 ounces and a standard deviation of 3 ounces. Use t

Question 1203848: The Acme Company manufactures widgets. The distribution of widget weights is bell-shaped. The widget weights have a mean of 56 ounces and a standard deviation of 3 ounces.
Use the Empirical Rule.
Suggestion: sketch the distribution in order to answer these questions.
a) 68% of the widget weights lie between
and

b) What percentage of the widget weights lie between 50 and 59 ounces?
%
c) What percentage of the widget weights lie below 65 ?
%
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
the empirical rule graph is shown below:

your mean is 56 and your standard deviation is 3.

plus or minus 1 standard deviations gets you a raw score of 56 plus or minus 3 which is between 53 and 59.

plus or minus 2 standard deviations gets you a raw score of 56 plus or minus 6 which is between 50 and 62.

plus or minus 3 standard deviations gets you a raw score of 56 plus or minus 9 which is between 47 and 65.

i redid the graph to show the raw scores.
it is shown below.

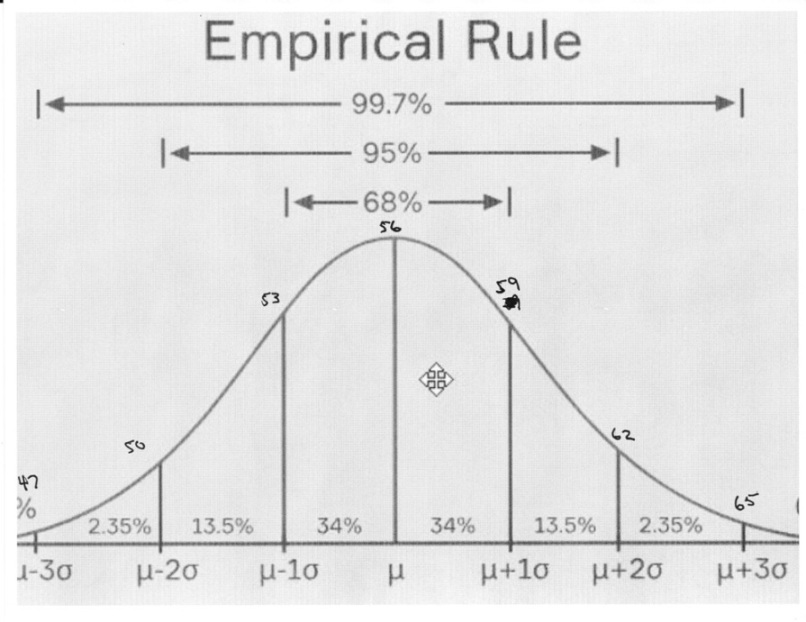
a) 68% of the widget weights lie between 53 and 59.

b) What percentage of the widget weights lie between 50 and 59 ounces?

looks like 13.5 + 34 + 34 = 81.5%

c) What percentage of the widget weights lie below 65 ?

looks like 2 * (34 + 13.5 + 2.35) = 2 * 49.85) = 99.7% , but there's a small piece on the left end that hasn't been accounted for.
the normal curve has 100% of the area below it from the extreme left side to the extreme right side.
3 standard deviations is 99.7% of it.
that leave .3% outside the 99.7% interval.
half of it is on the left side and half of it is on the right side.
that leaves .15% on each end that is outside of the plus or minus 3 standard deviations area.
area to the left of 65 includes the left edge of .15% that hasn't been counted yet, so the percent of the widget weights that lie below 65 is 99.7% + .15% = 99.85%.

RELATED QUESTIONS
Business. A small company has an assembly line that produces three types of widgets. The (answered by ikleyn)

The distribution of weights of a sample of 1400 cargo containers is symmetric and bell... (answered by Boreal)

A company has two machines that make widgets. The production costs are listed below. Find (answered by josmiceli)

ABC Widgets sell two types of widgets. The Wonder Widget sells for $15 and the Mighty... (answered by josgarithmetic,greenestamps)

widget A = 6 widget B = 10 (Total widgets = 16) With 6 random samples of the total... (answered by Boreal)

The engineer in a widget factory wants to test out a new form of raw materials. So a... (answered by stanbon)

Need help having problems solving this problem The engineer in a widget factory wants... (answered by stanbon)

The engineer in a widget factory wants to test out a new form of raw materials. So a... (answered by stanbon)

Fred�s Widget Company wants to make sure his widgets are within the weight tolerances he... (answered by stanbon)