SOLUTION: SAT scores are normally distributed with a mean of 1,500 and a standard deviation of 300. An administrator at a college is interested in estimating the average SAT score of first-y

Question 1202134: SAT scores are normally distributed with a mean of 1,500 and a standard deviation of 300. An administrator at a college is interested in estimating the average SAT score of first-year students. If the administrator would like to limit the margin of error of the 86% confidence interval to 15 points, how many students should the administrator sample? Make sure to give a whole number answer.

Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
mean is 1500
standard deviation is 300
confidence interval is .86
standard error = standard deviation / square root of sample size = s/sqrt(n)
s is the standard error
n is the sample size
they want to limit the margin of error to less than or equal 15 points.
z-score formula is z = (x-m)/s
x is the sample mean
m is the population mean
s is the standard error
(x-m) is the margin of error
with (x-m) equal to 15, the formula becomes:
z = 15 / s
at 86% confidence interval, the critical z-score is plus or minus 1.475791028.
the formula becomes:
1.475791028 = 15 / s
s = standard error = standard deviation / square root of sample size = 300/ sqrt(n).
the formula becomes:
1.475791028 = 15 / (300 / sqrt(n))
simplify to get:
1.475791028 = 15 / 300 * sqrt(n)
solve for sqrt(n) to get:
sqrt(n) = 1.475791028 * 300 / 15 = 29.51582055.
when sqrt(n) = 29.51582055, s = 300 / 29.51582055 = 10.16404065.
when s = 10.16404065, the z-score formula becomes 1.475791028 = (x-m) / 10.16404065
solve for (x-m) to get:
(x-m) = 1.475791028 * 10.16404065 = 15.
margin of error = 15 is confirmed to be accurate using the normal distribution calculator at https://www.hackmath.net/en/calculator/normal-distribution
the results are shown below.

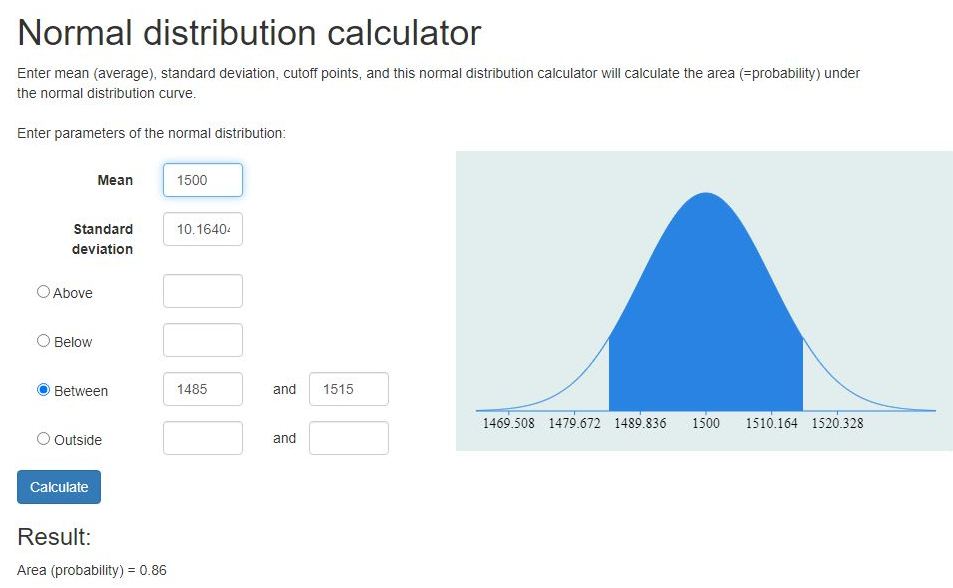
the mean was input as 1500.
the standard error was input as 10.16404065.
the square root of n was equal to 29.51582055.
you can see that the margin of error was plus or minus 15 because the 86% confidence interval was from 1485 to 1515.
solve for n to get n = sqrt(n) squared = 871.183663.
round that to the next higher integers to get n = 872.
that would be the minimum sample size for the margin of error to be less than 15.

RELATED QUESTIONS
SAT scores are normally distributed with a mean of 1,500 and a standard deviation of 300. (answered by Boreal)

SAT scores are normally distributed with a mean of 1,500 and a standard deviation of 300. (answered by Boreal)

SAT scores are distributed with a mean of 1,500 and a standard deviation of 300. You are... (answered by ewatrrr)

The College Board reports that the nationwide mean SAT Math score was 515 in 2007. Assume (answered by stanbon)

Based on data from the College board SAT scores are normally distributed with a mean of... (answered by Boreal)

SAT I scores around the nation tend to have a mean scale score around 500, a standard... (answered by stanbon)

assume that math sat scores are normally distributed with a mean of 500 and a standard... (answered by lynnlo)

5 In exercises 5-8 assume that SAT scores are normally distributed with mean u=1518 and... (answered by tommyt3rd)

#3 SAT scores are distributed with a mean of 1,500 and a standard deviation of 300. You... (answered by Boreal)