Question 1202084: A sales tax officer has reported that the average sales of the 500 business that he has to deal with during a year is Rs.36,000 with a standard deviation of 10,000. Assuming that the sales in these business are normally distributed find (i) The number of business as the sales of which are greater than RS. 40,000 (ii) The percentage of business of which are likely to range between Rs. 30,000 and Rs. 40,000.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! average sales of 500 businesses is 36000 with standard deviation of 10000.
z-score formula is z = (x-m)/s
z is the z-score.
x is the raw score.
m is the mean.
s is the standard deviation.
Assuming that the sales in these business are normally distributed find:
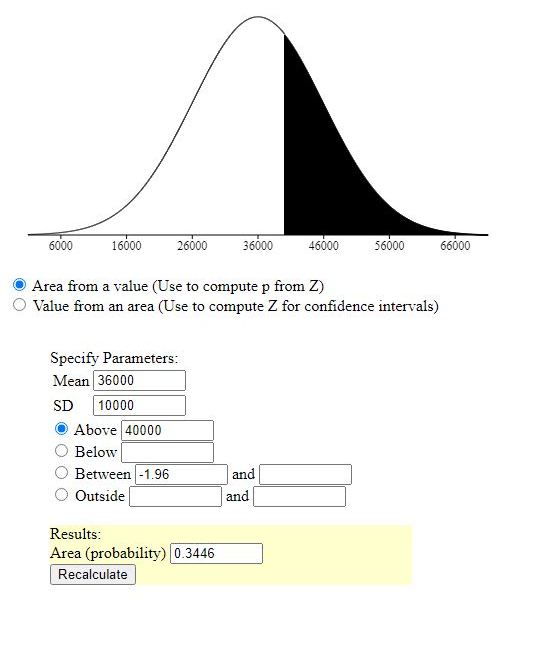
(i) The number of business as the sales of which are greater than RS. 40,000.
use the z-score formula.
m = 36,000
s = 10,000
x = 40,000
z = (x-m)/s = (40,000 - 36,000) / 10,000 = .4
area to the right of that z-score is equal to .3445783029.
multiply that by 500 to get 172.2891515 businesses that have sales greater than 40,000.
round to the nearest integer to get 172.
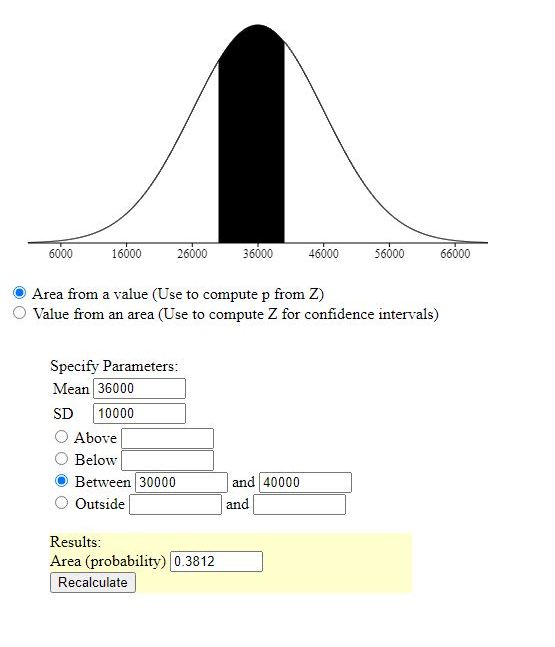
(ii) The percentage of business of which are likely to range between Rs. 30,000 and Rs. 40,000.
z-score for 30,000 = (30,000 - 36,000) / 10,000 = -.6
z-score for 40,000 = (40,000 - 36,000) / 10,000 = .4
area to the left of z-score of -.6 = .2742530646.
area to the left of z-score of .4 = .6554216971
area in between is the larger area minus the smaller area = .3811686325.
multiply that by 500 to get 190.5843162.
round to the nearest integer to get 191.
herre's what the percentages look like on a z-score calculator.
greater than 40,000 is first.
between 30,000 and 40,000 is second,.
calculator used is found at https://davidmlane.com/hyperstat/z_table.html
|
|
|