mu = population mean
sigma = population standard deviation
n = sample size
xbar = sample mean
Hypothesis:
Ho: mu = 900
Ha: mu =/= 900
The "not equals" sign in the alternative hypothesis tells us that we're doing a two-tailed test.
Other given info
sigma = 150
n = 40
xbar = 942
Compute the test statistic.
z = (xbar - mu)/(sigma/sqrt(n))
z = (942 - 900)/(150/sqrt(40))
z = 1.7708754896943
z = 1.77
Notice I used the Z statistic instead of T statistic.
This is valid for two reasons
- We were given the value of sigma.
- The sample size is larger than 30. When n > 30, the T distribution starts to look like the Z distribution (approximately). Refer to the Central Limit Theorem for more information. This relevant article is also something I recommend for further reading.
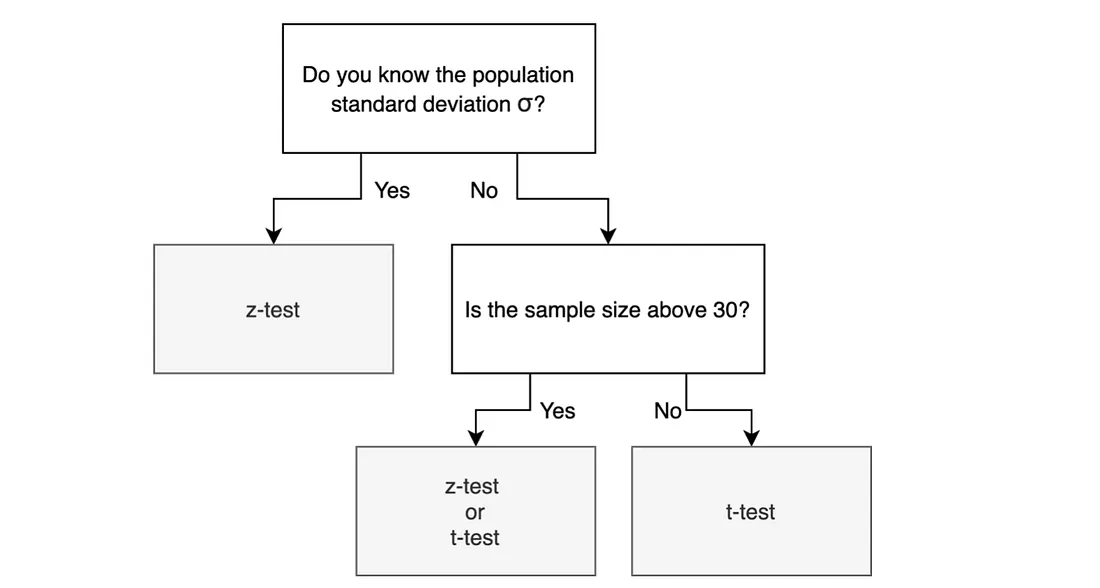
Image Source
https://towardsdatascience.com/introduction-tfrom-the-central-limit-theorem-to-the-z-and-t-distributions-66513defb175
Now use a table such as this one
https://www.ztable.net/
to find that
P(Z < 1.77) = 0.96164
Or you can use a stats calculator for better accuracy.
This then leads to
P(Z > 1.77) = 1 - P(Z < 1.77)
P(Z > 1.77) = 1 - 0.96164
P(Z > 1.77) = 0.03836
This is the approximate area under the standard normal curve to the right of z = 1.77
Because we're doing a two-tailed test, we'll double that result
2*0.03836 = 0.07672
This represents the p-value.
Rule: If the p-value is smaller than alpha, then we reject the null.
A handy memorization phrase could be "If the p-value is low, then the null must go".
Since the p-value (0.07672) is NOT smaller than alpha = 0.05, we fail to reject the null.
Therefore, the null is "accepted". I put that in quotes because technically we haven't accepted it. Rather we just haven't found enough evidence to reject it, so we have no choice but to side with the null.
Your answer of "Ho is accepted" is correct.
One interpretation would be The sample battery life is not significantly different from 900 days
In other words,The average lifespan of a cellphone battery appears to be 900 days
Side notes:
- 900 days = 900/365 = 2.4658 years (approximate)
- 0.4658 years = 0.4658*365 = 170.017 = 170 days (approximate)
- 2.4658 years = 2 years + 0.4658 years = 2 years + 170 days (approximate)
- Therefore, 900 days = 2 years + 170 days (approximate)
- This is ignoring leap years.