Question 1196701: #1 spinner circle is half green, 1/4 red and 1/4 blue. #2 spinner circle is half red, the other half has green, red, and yellow in equal sections.
If you get the same color twice, what is the probability it was red? green?
Thanks
Found 3 solutions by math_tutor2020, ikleyn, greenestamps:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
spinner A: 1/2 green, 1/4 red, 1/4 blue
spinner B: 2/3 red, 1/6 green, 1/6 yellow
Note: if spinner B has half red on one side, and a 1/6 slice of red on the other side, then 1/2+1/6 = 3/6+1/6 = 4/6 = 2/3 is how much of a fraction red takes up in total.
P(2 green) = P(A is green)*P(B is green)
P(2 green) = (1/2)*(1/6)
P(2 green) = 1/12
P(2 red) = P(A is red)*P(B is red)
P(2 red) = (1/4)*(2/3)
P(2 red) = 2/12
P(2 blue) = P(A is blue)*P(B is blue)
P(2 blue) = (1/4)*(0)
P(2 blue) = 0
It is impossible to get 2 blue since spinner B does not have blue.
P(2 yellow) = P(A is yellow)*P(B is yellow)
P(2 yellow) = (0)*(2/3)
P(2 yellow) = 0
It is impossible to get 2 yellow since spinner A does not have yellow.
So either we get 2 red or 2 green if we want two of the same color.
P(2 same color) = P(2 red OR 2 green)
P(2 same color)= P(2 red) + P(2 green)
P(2 same color) = 2/12 + 1/12
P(2 same color) = (2 + 1)/12
P(2 same color) = 3/12
P(2 same color) = 1/4
Note: The events "2 red" and "2 green" are mutually exclusive.
Then we can say
P(2 red, given 2 of the same color) = P(2 red)/P(2 same color)
P(2 red, given 2 of the same color) = (2/12)/(1/4)
P(2 red, given 2 of the same color) = (2/12)*(4/1)
P(2 red, given 2 of the same color) = 8/12
P(2 red, given 2 of the same color) = 2/3
And,
P(2 green, given 2 of the same color) = P(2 green)/P(2 same color)
P(2 green, given 2 of the same color) = (1/12)/(1/4)
P(2 green, given 2 of the same color) = (1/12)*(4/1)
P(2 green, given 2 of the same color) = 4/12
P(2 green, given 2 of the same color) = 1/3
The results 2/3 and 1/3 are complementary to represent all the possible ways to get 2 of the same color. For more information, check out the concept of conditional probability.
------------------------------------------------------------
Another approach:
We can use table to lay out the possible outcomes.
Along the top row are the four slices of green, green, red and blue for spinner A.
The outcomes for spinner B are along the left hand side.
| | 1 | 2 | 3 | 4 | | | green | green | red | blue | | 1 | red | | | X | | | 2 | red | | | X | | | 3 | red | | | X | | | 4 | red | | | X | | | 5 | red | | | X | | | 6 | red | | | X | | | 7 | green | X | X | | | | 8 | green | X | X | | | | 9 | red | | | X | | | 10 | red | | | X | | | 11 | yellow | | | | | | 12 | yellow | | | | |
Each X represents a situation where we get 2 of the same color. Either 2 red or 2 green. The cells left blank are when we get a mix of two different colors, so we'll ignore those cases. The numbers along the left and top are there to help keep track of the slices.
There are 12 X's total.
Four of the Xs are when we get 2 greens
4/12 = 1/3
while the remaining eight are 2 reds
8/12 = 2/3
------------------------------------------------------------
Answers:
If we get 2 of the same color, then,
probability of 2 reds = 2/3
probability of 2 greens = 1/3
Answer by ikleyn(52788)  (Show Source):
You can put this solution on YOUR website! .
#1 spinner circle is half green, 1/4 red and 1/4 blue.
#2 spinner circle is half red, the other half has green, red, and yellow in equal sections.
If you get the same color twice, what is the probability it was
(a) red?
(b) green?
~~~~~~~~~~~~~~~~
For spinner 1, we have these probabilities/events
P(G1) = 1/2 (green); P(R1) = 1/4 (red); P(B1) = 1/4 (blue).
For spinner 2, we have these probabilities/events
P(G2) = 1/6 (green); P(R2) = 1/2 + 1/6 = 4/6 = 2/3 (red); P(Y2) = 1/6 (yellow).
The probability to have same color twice in two spinners is
P = P(G1,G2) + P(R1,R2) =  +  =  =  =  .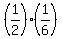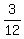
Then the ANSWER to question (a) is P(R1,R2)/P =  =  =  .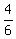
The ANSWER to question (b) is P(G1,G2)/P =  =  =  .
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Grammatically, the statement of the problem is flawed. "If you get the same color twice..." implies that you are doing something twice -- e.g., spinning one of the spinners twice. But the apparent intent of the question is that EACH spinner is spun ONCE.
Overlooking that shortcoming with the statement of the problem....
Only the red and green colors are on both spinners, so note that the sum of the answers to the two questions must be 1.
Spinner #1 is 1/4 red; spinner #2 is (1/2+1/6) = 2/3 red. The probability of getting red on both spinners is (1/4)(2/3) = 2/12.
Spinner #1 is 1/2 green; spinner #2 is 1/6 green. The probability of getting green on both spinners is (1/2)(1/6) = 1/12.
So the probability of getting the same color on both spinners is (2/12)+(1/12) = 3/12.
Then the CONDITIONAL probability that you get red on both spinners, GIVEN THAT you got the same color on both spinners, is (2/12)/(3/12) = 2/3.
And the conditional probability that you get green on both spinners, given that you got the same color on both spinners, is (1/12)/(3/12) = 1/3.
ANSWERS: red 2/3; green 1/3
And note that the sum of the two answers is 1, as it must be....
|
|
|
