Question 1192102: Sketch a normal curve for each distribution. Label the x-axis at one, two, and three standard deviations from the mean.
1. Mean = 30; Standard deviation = 5
2. Mean = 95; Standard deviation = 12
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll do problem 1 to get you started.
Draw a bell curve as shown below. At the very center, where the hill is at its peak, we have the mean = 30.
The gap between adjacent tickmarks is a gap of 1 standard deviation, which in this case is 5 units.
In other words, the gap between any adjacent tickmarks is 5 units.
If we started at the center (mean = 30) and moved 1 tickmark or standard deviation to the right, then we arrive at 30+5 = 35.
Another tickmark over and we arrive at 30+2*5 = 40
and so on
The same idea applies in reverse when going to the left.
Start at mean = 30 and move 1 tickmark to the left to get to 30-5 = 25
Then another tick over and we get to 30-2*5 = 20
and so on.
Standard convention is to do 3 standard deviations away from the mean (which accounts for roughly 99.7% of the normally distributed population; according to the Empirical Rule)
This accounts for the following tickmarks on the x axis:
15, 20, 25, 30, 35, 40, 45
This is what the final sketch should look like

I used GeoGebra to make the figure, which is free software. I encourage this route as well, or any free online software that offers similar capabilities.
Though if your teacher wants you to sketch by hand, then be sure to follow those instructions of course.
If you wanted, you can add in the labels shown in blue

to get a better sense of what each location is.
Something like 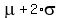 means we're 2 standard deviations above the mean means we're 2 standard deviations above the mean
While another example like 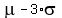 indicates we're now 3 standard deviations below the mean. indicates we're now 3 standard deviations below the mean.
 = greek letter mu = mean = greek letter mu = mean
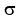 = greek letter sigma = standard deviation = greek letter sigma = standard deviation
Optionally you can add in vertical lines to help better separate the various pieces or sections.

The vertical lines also help show the markers of each standard deviation distance from the center mean.
Side note: the vertical lines at 15 and 45 are barely noticeable. These locations are 3 standard deviations away from the mean.
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In the web-page
https://www.quora.com/How-do-you-plot-a-normal-distribution-in-Excel-with-mean-and-standard-deviation
you will find a complete description on how to plot a normal curve in Excel
with the given mean and the given standard deviation.
To plot a normal distribution in Excel with mean and standard deviation, you can follow these steps:
1. Enter the mean and standard deviation values in separate cells.
2. In another cell, enter the formula "=NORM.DIST(x,mean,sd,0)" where "x" is the value
for which you want to calculate the normal distribution probability, "mean" is the mean value
you entered in step 1, "sd" is the standard deviation value you entered in step 1,
and "0" indicates that you want the cumulative distribution function.
3. Copy the formula from step 2 and paste it into the cells below to calculate the normal distribution probabilities
for different values of "x".
4. Select the range of cells containing the normal distribution probabilities, including the cell
with the formula in step 2.
5. Click on the "Insert" tab in the ribbon.
6. Click on the "Recommended Charts" button.
7. Select the "All Charts" tab.
8. Click on the "Statistical" category.
9. Select the "Normal Distribution" chart type.
10. Click "OK" to create the chart.
|
|
|