SOLUTION: Six women and five men walk into an appliance store at the same time. There are five salesperson available to help them. Find the probability that the salesperson will first hepl a

Click here to see ALL problems on Probability-and-statistics

Question 1190403: Six women and five men walk into an appliance store at the same time. There are five salesperson available to help them. Find the probability that the salesperson will first hepl at least two women
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

In an obscure way, the problem is asking what the probability is that, of the first 5 customers helped, either 2 or 3 or 4 or 5 are women.

The customers are 6 women and 5 men, so the probability that any one woman is helped is 6/11 and the probability that any one man is helped is 5/11.

We could find the answer by computing the probabilities of having only 0 or 1 women among the first 5 helped and subtract that from 1.

Or we could find the answer by computing the probabilities that 2 to 5 women are among the first 5 helped and add those.

But for learning purposes, I would suggest that it is useful to compute the probabilities for ALL the cases. That is only a bit more work than is required; it gives the student practice in computing such probabilities; and it gives the student a check on his computations by verifying that the sum of the probabilities for all the cases is 1.

So let's do that. Since we want to verify that the sum of all the probabilities is 1, we will leave each probability in exact fraction form rather than in approximate decimal form.

P(0 women):

P(1 woman):

P(2 women):

P(3 women):

P(4 women):

P(5 women):

Verify that the sum of the probabilities is 1:

The probabilities for the different cases are correct, so we can find the answer to the problem:

ANSWER: The probability that among the first 5 customers served at least 2 are women is

Answer by ikleyn(52790)   (Show Source):
You can put this solution on YOUR website!
.
Six women and five men walk into an appliance store at the same time.
There are five salesperson available to help them.
Find the probability that the salesperson will first hepl at least two women
~~~~~~~~~~~~~~~~~~~

            I read, understand and interpret the problem in this way:

+----------------------------------------------------------------------+ | Find the probability that among 5 people, randomly selected | | | | from the set of 6 women and 5 men, there are at least two women. | +----------------------------------------------------------------------+

            Below is the solution to the problem formulated in this way.

In total, there are 6+5 = 11 persons. The total number of all different quintuples (groups of 5 persons, randomly selected from 11 people) is total = 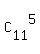= = 462. It is the size of the space of events. It is the denominator of the probability fraction. Of all these quintuples, the favorable are those that contain 2, or 3, or 4, or 5 women. So, the favorable quintuples are (2w,3m), (3w,2m), (4w,1m), (5w,0m). THEREFORE, the number of favorable quintuples is favorable = = 15*10 + 20*10 + 15*5 + 6*1 = 431. The probability under the problem question (as I understand/interpret it) is this ratio P = = = = 0.9329 (rounded). ANSWER

Solved.

--------------

The solution by the other tutor is incorrect.