(a) Calculate the value of z for Ho: 𝜇 = 10, 𝜎 = 3.1, n = 41, x = 11.5.
mean = m = 10
standard deviation = sd = 3.1
sample size = n = 41
sample mean = x = 11.5
standard error = s = standard deviation divided by square root of sample size = 3.1 / sqrt(41) = .484139 rounded to 6 decimal places.
z = (x - m) / s = (11.5 - 10) / .484139 = 3.098283757.
round to two decimal places to get z = 3.1
(b) Calculate the value of z for Ho: 𝜇 = 120, 𝜎 = 27, n = 30, x = 126.3.
mean = m = 120
standard deviation = sd = 27
sample size = n = 30
sample mean = x = 126.3
standard error = s = standard deviation divided by square root of sample size = 27 / sqrt(30) = 4.92950 rounded to 5 decimal places.
z = (x - m) / s = (126.3 - 120) / 4.92950 = 1.2167161984.
round to two decimal places to get z = 1.22.
(c) Calculate the value of z for Ho: 𝜇 = 18.2, 𝜎 = 3.7, n = 138, x = 18.89.
mean = m = 18.2
standard deviation = sd = 3.7
sample size = n = 138
sample mean = x = 18.89
standard error = s = 3.7 / sqrt(138) = .314965 rounded to 6 decimal places.
z = (x - m) / s = (18.89 - 18.2) / .314965 = 2.190719602.
round to two decimal places to get z = 2.19.
(d) Calculate the value of z for Ho: 𝜇 = 81, 𝜎 = 13.1, n = 53, x = 80.3.
mean = m = 81
standard deviation = sd = 13.1
sample size = n = 53
sample mean = x = 80.3
standard error = s = 13.1 / sqrt(53) = 1.799423 rounded to 6 decimal places.
z = (x - m) / s = (80.3 - 81) / 1.799423 = -.3890135894.
round to two decimal places to get z = -.39
here's a calculator that does all the dirty work for you.
https://www.calculatorsoup.com/calculators/statistics/z-score-calculator.php
i used this calculator on each of your problems.
your results are repeated below with the addition of the calculator results to show you that would get the same answer when using the calculator.
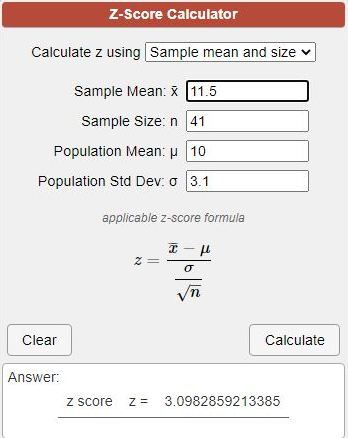
(a) Calculate the value of z for Ho: 𝜇 = 10, 𝜎 = 3.1, n = 41, x = 11.5.
mean = m = 10
standard deviation = sd = 3.1
sample size = n = 41
sample mean = x = 11.5
standard error = s = standard deviation divided by square root of sample size = 3.1 / sqrt(41) = .484139 rounded to 6 decimal places.
z = (x - m) / s = (11.5 - 10) / .484139 = 3.098283757.
round to two decimal places to get z = 3.1
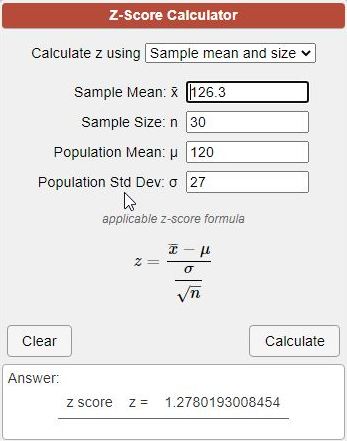
(b) Calculate the value of z for Ho: 𝜇 = 120, 𝜎 = 27, n = 30, x = 126.3.
mean = m = 120
standard deviation = sd = 27
sample size = n = 30
sample mean = x = 126.3
standard error = s = standard deviation divided by square root of sample size = 27 / sqrt(30) = 4.92950 rounded to 5 decimal places.
z = (x - m) / s = (126.3 - 120) / 4.92950 = 1.278020083
round to two decimal places to get z = 1.28.
(c) Calculate the value of z for Ho: 𝜇 = 18.2, 𝜎 = 3.7, n = 138, x = 18.89.
mean = m = 18.2
standard deviation = sd = 3.7
sample size = n = 138
sample mean = x = 18.89
standard error = s = 3.7 / sqrt(138) = .314965 rounded to 6 decimal places.
z = (x - m) / s = (18.89 - 18.2) / .314965 = 2.190719602.
round to two decimal places to get z = 2.19.

(d) Calculate the value of z for Ho: 𝜇 = 81, 𝜎 = 13.1, n = 53, x = 80.3.
mean = m = 81
standard deviation = sd = 13.1
sample size = n = 53
sample mean = x = 80.3
standard error = s = 13.1 / sqrt(53) = 1.799423 rounded to 6 decimal places.
z = (x - m) / s = (80.3 - 81) / 1.799423 = -.3890135894.
round to two decimal places to get z = -.39.
