SOLUTION: Suppose events A and B are independent and P(A) = 1/4 P(B) = 1/5 Find the probability. (Enter the probability as a fraction.) ____

Click here to see ALL problems on Probability-and-statistics

Question 1186068: Suppose events A and B are independent and
P(A) = 1/4

P(B) = 1/5
Find the probability. (Enter the probability as a fraction.)
_____
P(A ∩ B) the line is above a and b only

Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Since events A and B are independent, the probability of both A and B occurring (their intersection) is simply the product of their individual probabilities:
P(A ∩ B) = P(A) * P(B)
Given P(A) = 1/4 and P(B) = 1/5, we have:
P(A ∩ B) = (1/4) * (1/5) = 1/20
So the answer is $\boxed{1/20}$.

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

Suppose events A and B are independent and P(A) = 1/4 P(B) = 1/5 Find the probability. (Enter the probability as a fraction.) _____ P(A ∩ B) the line is above a and b only
~~~~~~~~~~~~~~~~~~~~~~~~

        The solution in the post by @CPhill is incorrect,
        since he incorrectly reads/interprets the problem.

The fact that " the line is above A and B only " means, that the question is about P(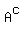 ∩ 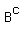), where 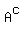is the complement to A and 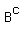is the complement to B. We have then = 1 - 1/4 = 3/4 and = 1 - 1/5 = 4/5. Since events A and B are independent, the events 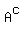and 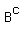are independent, too. Therefore, P(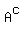 ∩ 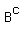)}}} = = = . ANSWER

Solved correctly.

SOLUTION: Suppose events A and B are independent and P(A) = 1/4 P(B) = 1/5 Find the probability. (Enter the probability as a fraction.) _____ P(A ∩ B) the line is above