SOLUTION: Let us assume that the grades of 500 students are normally distributed with 𝜇=45 and standard deviation 𝜎=20. If the 20% of the students get excellent, what is the grade that

Question 1185779: Let us assume that the grades of 500 students are normally distributed with 𝜇=45 and standard deviation 𝜎=20. If the 20% of the students get excellent, what is the grade that determines the excellent? (What is 𝛸 value?)
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
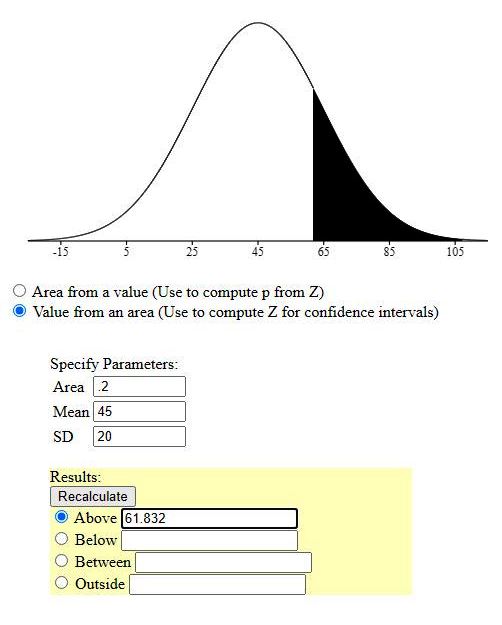
mean = 45
standard deviation = 20
number of students = 500

z-score = (x - m) / s

in this problem:

x is the number of students who get excellent.
m is the mean = 45
s is the standard deviation = 20

you are looking for the z-score that has 20% of the area of the normal distribution curve to the right of it.

that z-score will be equal to .8416 when rounded to 4 decimal places.

to find the raw score, use the z-score formula of z = (x - m) / s

in this formula, z = .8416, m = 45, s = 20

the formula becomes .8416 = (x - 45) / 20

solve for x to get:

x = .8416 * 20 + 45 = 61.832.

a score above that will be excellent.
only 20% of the students will get a score greater than that.

RELATED QUESTIONS
Let us assume that the grades of 500 students are normally distributed with 𝜇=45 and... (answered by Edwin McCravy)

Let us assume that the grades of 500 students are normally distributed with 𝜇=45 and... (answered by Boreal)

The final grades of students in Foreign Language are normally distributed. records show... (answered by CPhill)

assume that math sat scores are normally distributed with a mean of 500 and a standard... (answered by lynnlo)

A professor at a local university noted that the grades of her students were normally... (answered by stanbon)

Assume the random variable X is normally distributed with mean muequals50 and standard... (answered by Boreal)

Assume that the heights of 3000 male students at a university are normally distributed... (answered by Alan3354)

The distribution of grades on a certain test has a mean of 85.5 with a standard deviation (answered by Boreal)

A standardized test is designed so that the scores are normally distributed with a mean... (answered by dfrazzetto)