SOLUTION: A distribution of values is normal with a mean of 63.6 and a standard deviation of 14.4.
Find the probability that a randomly selected value is greater than 44.9.
P(X > 44.9) =
Algebra.Com
Question 1185731: A distribution of values is normal with a mean of 63.6 and a standard deviation of 14.4.
Find the probability that a randomly selected value is greater than 44.9.
P(X > 44.9) =
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
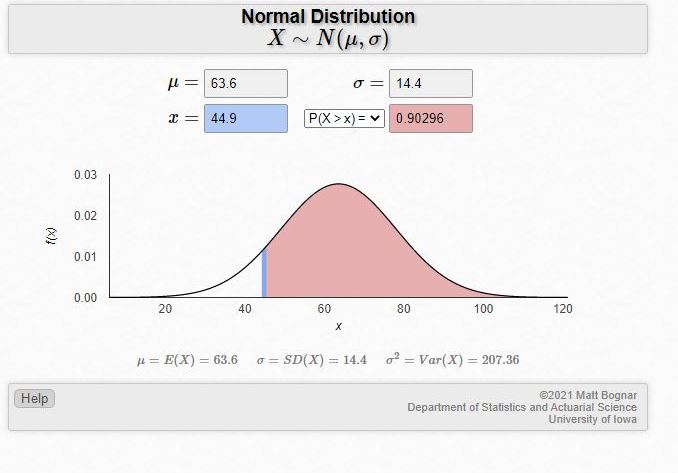
the mean is 63.6
the standard deviation is 14.4
my ti-84 plus calculator will tell you that the probability that a randomly selected value is greater than 44.9 is .9029612237.
this online calculator will tell you that the probability is .90296.
they both say the same thing with the only difference being in the number of decimal digits being rounded to.
here's what the results from the online calculator show you.
RELATED QUESTIONS
Suppose you have a normal distribution of values with a mean of 70 and a standard... (answered by mathmate)
A distribution of values is normal with a mean of 231.6 and a standard deviation of 62.4.
(answered by stanbon)
A distribution of values is normal with a mean of 148.3 and a standard deviation of 92.3.
(answered by Theo)
Some probability distributions. Here is a probability distribution for a random variable... (answered by CPhill)
let x have a normal distribution with mean of 24 and standard deviation of 6 find the... (answered by ewatrrr)
If random samples of size 9 is taken from a normal distribution with mean 50 and standard (answered by stanbon)
In a normal distribution the mean is 50 and the standard deviation is 5. Find the... (answered by reviewermath)
A distribution of values is normal with a mean of 144 and a standard deviation of 73.2.
(answered by Theo)
A normal distribution of mean 5 and standard deviation 3. What is the probability that... (answered by stanbon)
