Question 1185493: A set of exam scores is normally distributed with a mean = 74 and standard deviation = 4.
Use the Empirical Rule to complete the statements below:
A) ___% of the exam scores are less than or equal to 74.
B) ___% of the exam scores are less than or equal to 70.
C) ___% of the exam scores are less than or equal to 82.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the empirical rule states that:
68% of the scores are within 1 standard deviation from the mean.
95% of the scores are within 2 standard deviations from the mean.
99.7% of the scores are within 3 standard deviations from the mean.
50% of the scores are below the mean and 50% of the scores are above the mean.
from this information, you can construct your own table as shown below:
34% of the scores are within 1 standard deviation below the mean and 34% of the scores are within 1 standard deviation above the mean.
47.5% of the scores are within 2 standard deviations below the mean and 47.5% of the scores are within 2 standard deviations above the mean.
49.85% of the scores are within 3 standard deviations below the mean and 49.85% of the scores are within 3 standard deviations above the mean.
from this information, you can solve this problem without the need of a calculator.
the mean is 74 and the standard deviation is 4.
50% of the scores are less than 74.
since 34% of the scores are within 1 standard deviation below the mean, and since 70 is 1 standard deviation below the mean, then 34% of the scores are between 70 and 74.
that means that 50 minus 34 = 16% are below 70.
since 47.5% of the scores are within 2 standard deviations above the mean, and since 82 - 74 = 8 = 2 standard deviations above the mean, then 47.5% of the scores are between 74 and 82.
add 50 to that and you get 97.5% of the scores are below 82.
your solutions are:
A) 50% of the exam scores are less than or equal to 74.
B) 16% of the exam scores are less than or equal to 70.
C) 97.5% of the exam scores are less than or equal to 82.
the following picture will show you what i mean.

from the diagram, the mean is at 0 which corresponds to the mean of74.
70 is 1 standard deviation below the mean.
66 is 2 standard deviations below the mean.
62 is 3 standard deviations below the mean.
below 62 is more than 3 standard deviations below the mean.
78 is 1 standard deviation above the mean.
82 is 2 standard deviations above the mean.
86 is 3 standard deviations above the mean
higher than 86 is more than 3 standard deviations above the mean.
50% of the scores are below 74.
that would be 34% + 13.5% + 2.35% + .15% counting from 75 down.
in a normal distribution, 50% of the scores are below the mean and 50% of the scores are above the mean.
16% of the scores are below 70.
that would be 13.5% + 2.35% + .15% counting from 70 down.
97.5% of the scores are below 82.
that would be 13.5% + 34% + 34% + 13.5% + 2.35% + .15% counting from 82 down.
to show you that these figures are reasonable, i used an online z-score calculator to give you the more detailed percentage, which you will find are close to the rough estimates.

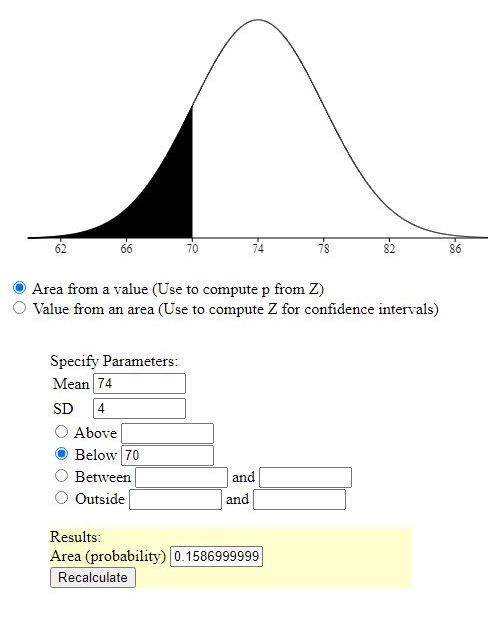

multiply the answers in the calculator by 100 and they become percents.
|
|
|