the formula to use is z = (x - m) / s
z is the z-score
x is the raw score
m is the mean
s is the standard error.
if you want the margin of error to be equal to 1, then (x - m) must be equal to 1.
the formula becomes:
z = 1 / s
at 90% confidence level, the two tailed condidence interval will require a cr5iticql z-score of plus or minus 1.645.
i usually work with the positive z-score to find the sample size required.
the formula becomes 1.645 = 1 / s.
s is equal to the population standard deviation divided by the square root of the sample size.
you get:
s = 2.5 / sqrt(n), where n is the sample size.
the formula becomes:
1.645 = 1 / (2.5 / sqrt(n)).
since 1 / (2.5 / sqrt(n)) is equal to 1 / 2.5 * sqrt(n), the equation becomes:
1.645 = 1 / 2.5 * sqrt(n).
multiply both sides of this equaton by 2.5 to get:
1.645 * 2.5 = sqrt(n).
solve for sqrt(n) to get:
sqrt(n) = 4.1125.
solve for n to get:
n = 16.91265625.
that's your solution.
since s is equal to 2.5 / sqrt(n), then s is equal to 2.5 / 4.1125 which makes s = .607903 rounded to 6 decimal places.
this value of the standard error = s will give you the margin of error you desire.
this margin of error will be the same, regardless of what the mean is.
some samples are shown below:
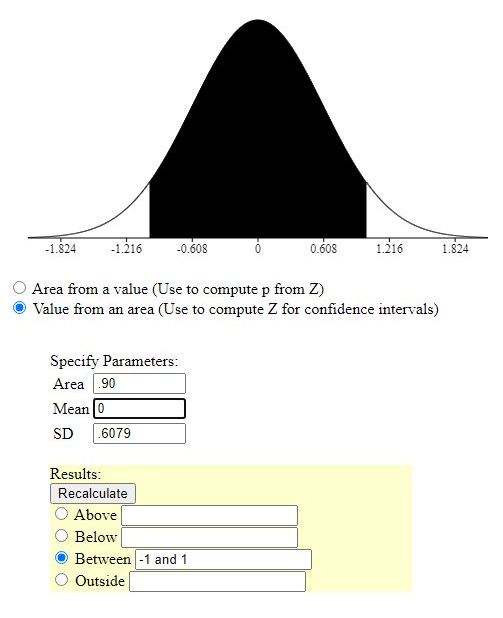


you can see that the margin of error is plus or minus 1 regardless of what the mean is.
for your second problem, i did the same thing.
critical z was still 1.645 because the confidence level was still 90%.
the margin of eror desired is not plus or minus .5.
the population standard deviation is now 2.4, rather than 2.5
the z-score formula ia still z = (x - m) / s
z is the z-score
x is the raw score
m is the mean
s is the standard error.
if you want a margin of error of .5, then (x - m) must be equal to .5.
the formula becomes:
1.645 = .5 / s
multiply both sides of the formula by s to get:
1.645 * s = .5
since s = 2.4 / sqrt(n), the formula becomes:
1.645 * 2.4 / sqrt(n) = .5
solve for sqrt(n) to get:
sqrtn) = 1.645 * 2.4 / .5
this makes sqrt(n) = 7.896
solve for n to get:
n = 7.896^2 = 62.346816.
when sqrt(n) = 7.896, then s = 2.4 / 7.896 = .3039513 rounded to 6 decimal places.
this is the standard error that will give you a margin of error of plus or minus .5 regardless of what the mean is.
some samples are shown below.



i believe you can generalize the formula as shown below.
the z-score formula is z = (x - m) / s
when (x - m) is the MOE, the formula becdomes:
z = MOE / s
multiply both sides of the formula by s to get:
z * s = MOE.
since s = population standard deviation / sqrt(n), the formula becomes:
z * population standard deviation / sqrt(n) = MOE.
solve for sqrt(n) to get:
sqrt(n) = z * population standard deviation / MOE.
let's see if this works.
when z = 1.645 and MOE = 1 and population standard deviation = 2.5, the formula becomes:
sqrt(n) = 1.645 * 2.5 / 1 = 4.1125.
this agrees with what we got before.
when z = 1.645 and MOE = .5 and population standard deviation = 2.4, the formula becomes:
sqrt(n) = 1.645 * 2.4 / .5 = 7.896.
this also agrees with what we got before.
the z-score used is the critical z-score for the confidence level indicated.