SOLUTION: Automatic is working with a standard deviation 1.5 g. It packs up tea in a pack with an average weight of 80 g. The average weight is 78.8 g. in a random sample of 16 packs. Does

Question 1177424: Automatic is working with a standard deviation 1.5 g. It packs up tea
in a pack with an average weight of 80 g. The average weight is 78.8 g. in a random sample of 16 packs. Does automatic need a tuning? A confidence level is 99%.
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
critical z-score is plus or minus 2.575829303.

standard error 1/5/sqrt(16) = 1.5/4 = .375

population mean is 80 grams.

sample mean is 78.8 grams.

sample z-score is equal to (78.8 - 80) / .375 = -3.2.

the two sided alpha for 99% confidence limit is equal to equal to .005.

the sample alpha is equal to .0006872020803.

the critical z-score is plus or minus 2.58
the critical alpha is equal to .005.

the sample z-score is equal to -3.2
the sample alpha is equal to .0007

the absolute value of the sample z-score is greater than the absolute value of the critical z-score.

the sample alpha is less than the critical alpha.

the test indicates that automatic definitely needs a tuning.

the very important calculation here is the calculation of the standard error.

that is equal to the population standard deviation divided by the square root of the sample size = 1.5/4 = .375.

the normal distribution curve in this problem looks like this.

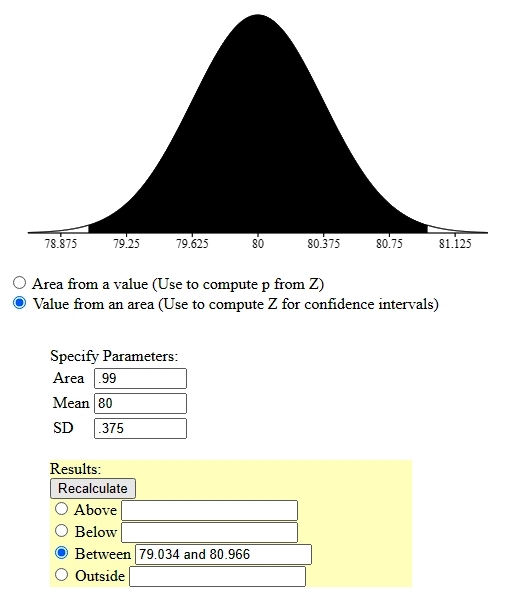
the display shows the 99% confidence level limits.
it's clear from the display that a sample mean of 78.8 is outside those limits.

RELATED QUESTIONS
The G.F packs 'shrimphs' in three categories:"small", Medium and Large, with average... (answered by stanbon)

Birth weights are normally distributed with a mean of 3421g and a standard deviation of... (answered by ewatrrr)

(Give your answers correct to TWO (2) decimal places) In a butter cookies packing... (answered by ewatrrr)

Julie sells 80 packets of tea. She makes a profit of $5 on each packet of green tea, and... (answered by richwmiller)

A manufacturer makes ball bearings that are supposed to have a mean weight of 30 g. A... (answered by bosley5580)

birth weights in the united states have a distribution that is approximately normal with... (answered by Boreal)

#1 (5 pts) 1. Forty percent of the Bowie State faculty teach online classes and 25% of... (answered by ewatrrr)

Please help me solve this, thank you! A random sample of 20 cans of milk showed an... (answered by ewatrrr)

A manufacturer claims that after using an automatic bottling plant, the average quantity... (answered by Boreal)