each question has 3 possible answers.
you are looking for the probability that the student guesses more than 75% of the questions correctly.
the probability of getting any one question correct is equal to 1/3.
the probability of getting any one question wrong is equal to 2/3.
this looks like a binomial distribution type problem.
the formula is:
p(x) = p^x * q^(n-x) * c(n,x)
x is the probability of getting it right.
q is the probability of getting it wrong.
n is the size of the set of possible selections.
x is the side of each subset of n.
when p = 1/3 and q = 2/3 and n = 24, then:
probability of getting more than 75% correct would be:
p(x) from x, where x > .75 * 24 = 3/4 * 24 = 18.
since 75% of 24 is 18, you would be looking for p(x) from x = 19 to 24.
the results are shown below:
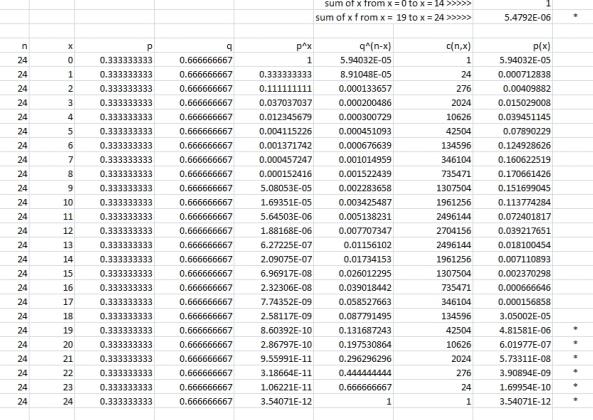
the probability from x = 19 to x = 24 is shown as 5.4792E-06.
that would be .0000054792.
round that to 3 decimal places and it becomes 0.
an example of one of the calculations is:
the probability of getting exactly 19 correct is:
p(19) = p^x * q^(n-1) * c(n,x) which becomes:
p(19) = (1/3)^19 * (1/3)^5 * c(24,19) which becomes:
p(19) = 4.81581359 * 10^6
that compares favorably to 4.81581E-06 in the excel spreadsheet which is the same answer rounded to 5 decimal places.
excel shows the rounded number, but uses the unrounded number.
c(n,x) is the combination formula.
for n = 24 and x = 19, the formula becomes c(24,19).
c(n,x) formula is n! / (x! * (n-x)!)
when n = 24 and x = 19, the formula becomes:
24! / (19! * 5!)
that can be written as (24 * 23 * 22 * 21 * 20 * 19!) / (19! * 5!)
the 19! in the numerator and the denominator cancels out and you are left with:
(24 * 23 * 22 * 21) / (5 * 4 * 3 * 2 * 1)
solve to get c(14,19) = 42504
that compares favorably to what is in the spreadsheet for p(19).
your results are the sum of p(19) to p(24).
the bottom line is, the probability of getting more than 75% correct is so low that it is effectively 0.
in excel, E-x means * 10^x.