Question 1157118: In how many ways can 4 letters be dropped in 3 mailboxes? How to calculate permutations?
Answer by ikleyn(52866)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In how many ways can 4 letters be dropped in 3 mailboxes? How to calculate permutations?
~~~~~~~~~~~~~~~~~~~
From the context, I assume that the letters are INDISTINGUISHABLE.
In other words, it is assumed that we distinct only amounts of letters in mailboxes.
It is a classic problem on bars and stars method.
You need to find the number of all NON-negative integer solutions of the equation
x1 + x2 + x3 = 4 (1)
Imagine 4 letters on the table, placed in one straight line with small gaps between them.
Imagine you have 4 numbered bars, of which you place the first bar (bar N1) before the first letter and the last bar (bar N4)
after the last letter in the row.
Let  , ,  , ,  be some solution to the given equation.
You then place bar N2 after be some solution to the given equation.
You then place bar N2 after  -th letter in the gap in the row of letters;
then you count next -th letter in the gap in the row of letters;
then you count next  letters in the row of letters after bar N2 and place bar N3 in the gap there;
The last letters in the row of letters after bar N2 and place bar N3 in the gap there;
The last  letters are between bars #3 and #4.
At this moment, all 4 letters are divided in 3 groups between bars (1-2), (2-3), and (3-4).
Notice that if some letters are between bars #3 and #4.
At this moment, all 4 letters are divided in 3 groups between bars (1-2), (2-3), and (3-4).
Notice that if some  is zero, then the corresponding bars go to the common respective gap.
So, having the solution to equation (1) in non-negative integer numbers, you place 2 bars, N2 and N3, in
their corresponding positions in gaps in the row of letters.
Vise versa, if you place 2 bars B2 and B3 in gaps in the row of 4 letters, you divide letters in 3 groups,
and the numbers of marbles in each group form the solution to equation (1).
Thus, there is one-to-one correspondence between the set of solutions to equation (1) in non-negative integer numbers,
from one side, and all different possible placings of 2 bars #2 and #3 in 2 gaps in the row between 4 letters.
Thus we have 4 + 2 = 6 entities, 4 letters and 2 movable bars #2 and #3; 4 letters are indistinguishable and 2 movable bars
are indistinguishable, too.
The number of all possible indistinguishable arrangements of 6 items of two types with 4 indistinguishable of one type
(letters) and 2 indistinguishable of the other type (bars) is is zero, then the corresponding bars go to the common respective gap.
So, having the solution to equation (1) in non-negative integer numbers, you place 2 bars, N2 and N3, in
their corresponding positions in gaps in the row of letters.
Vise versa, if you place 2 bars B2 and B3 in gaps in the row of 4 letters, you divide letters in 3 groups,
and the numbers of marbles in each group form the solution to equation (1).
Thus, there is one-to-one correspondence between the set of solutions to equation (1) in non-negative integer numbers,
from one side, and all different possible placings of 2 bars #2 and #3 in 2 gaps in the row between 4 letters.
Thus we have 4 + 2 = 6 entities, 4 letters and 2 movable bars #2 and #3; 4 letters are indistinguishable and 2 movable bars
are indistinguishable, too.
The number of all possible indistinguishable arrangements of 6 items of two types with 4 indistinguishable of one type
(letters) and 2 indistinguishable of the other type (bars) is
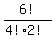 = = 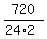 = 15.
Hence, the number of all possible solutions to equation (1) in non-nrgative integer numbers is 15.
ANSWER. The number of different placings of 4 letters in 3 mailboxes is 15. = 15.
Hence, the number of all possible solutions to equation (1) in non-nrgative integer numbers is 15.
ANSWER. The number of different placings of 4 letters in 3 mailboxes is 15.
Solved.
---------------
For the bars and stars method see this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_%28combinatorics%29
Notice that if the letters are distinguishable, then the solution and the answer are different.
|
|
|