SOLUTION: Suppose that the heights of adult women in the United States are normally distributed with a mean of 63.5 inches and a standard deviation of 2.3 inches. Jennifer is taller than 90%

Question 1150424: Suppose that the heights of adult women in the United States are normally distributed with a mean of 63.5 inches and a standard deviation of 2.3 inches. Jennifer is taller than 90% of the population of U.S. women. How tall (in inches) is Jennifer? Carry your intermediate computations to at least four decimal places. Round your answer to one decimal place.
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
mean = 63.5 inches
standard deviation = 2.3 inches.
jennifer is taller than 90% of the population of u.s. women.
how tall, in inches, is jennifer.
you can use the following calculator to solve this.
http://davidmlane.com/hyperstat/z_table.html
i did 3 calculations as shown below:

$$$

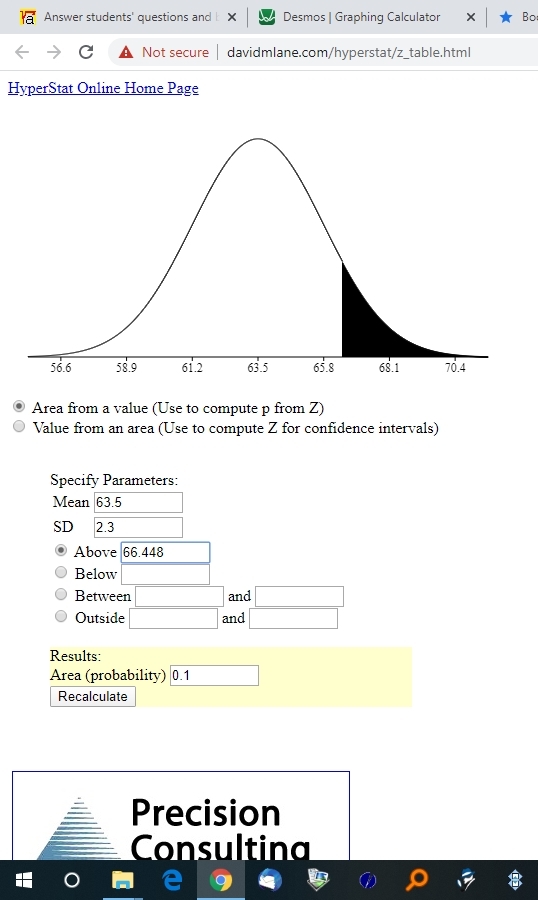
you put in the mean of 63.5 and the standard deviation of 2.3

the first display finds the raw score that has an area of .10 under the normal distribution curve to the right of it.

the second display finds the area to the right of the raw score.

you can also work this from z-scores.

first find the z-score that has 10% of the area under the normal distribution curve to the right of it.

using my ti-84 plus, i find that the z-score is 1.281551567 which can be rounded to 1.281551.

you then look for the area under the normal distribution curve to the right of that z-score to confirm this is accurate.

here's a display of that.
the mean is 0 and the standard is 1 when working with the z-score.

$$$

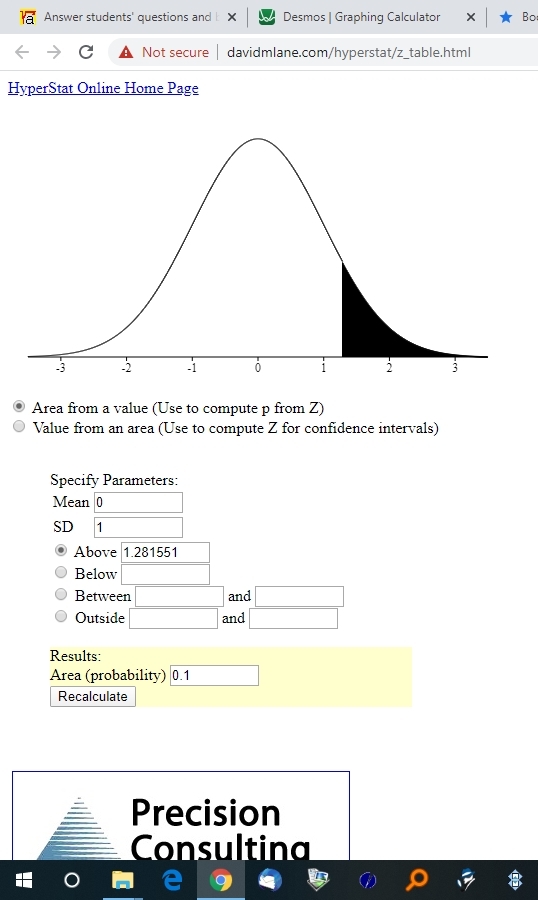
to find the raw score, use the z-score formula of z = (x - m) / s
z is the z-score
x is the raw score
m is the raw mean
s is the standard deviation, in this case.

formula becomes 1.281551 = (x - 63.5) / 2.3
solve for x to get:
x = 1.281551 * 2.3 + 63.5 = 66.4475 which can be rounded to 66.4.

as seen on the graph, the area to the right of that is .10.
the area to the left of that is 1 - .10 = .90.
that means that jennifer's height is greater than 90% of the group of girls whose mean height is 63.5 inches and whose standard deviation is 2.3 inches.

RELATED QUESTIONS
Suppose that the heights of adult women in the United States are normally distributed... (answered by stanbon)

Suppose that the heights of adult women in the United States are normally distributed... (answered by stanbon)

Need help Suppose that the heights of adult women in the United States are normally... (answered by vleith)

THis is homework can you help? Suppose that the heights of adult women in the United... (answered by Edwin McCravy)

can someone please help me solve this? thank you Suppose that the heights of adult... (answered by stanbon)

Assume that women have heights that are normally distributed with a mean of 63.6 inches... (answered by math_tutor2020)

Assume that women have heights that are normally distributed with a mean of 63.6 inches... (answered by Theo)

Assume that the heights of women are normally distributed with a mean of 63.6 inches and... (answered by ewatrrr)

Men's heights are normally distributed with a mean of 69.0 inches and a standard... (answered by ikleyn)