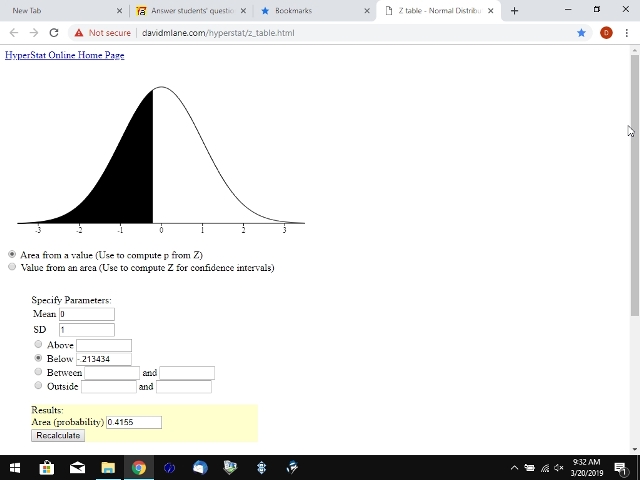
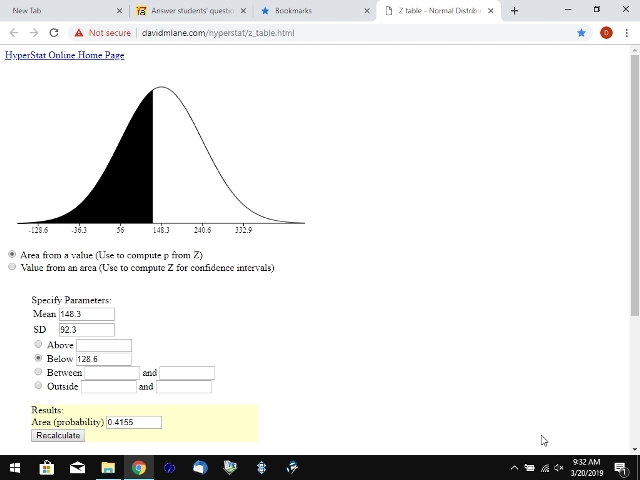
128.6 is equal to (148.3 - 128.6) / 92.3 = .2134344529 standard deviations below the mean.
since the mean in a z-score is 0 and the standard deviation in a z-score is equal to 1, then the z-score for 128.6 with a mean of 148.3 is equal to 0 - .2134344529 = -.2134344529.
you can confirm this using the z-score formula of z = (x - m) / s.
z is the z-score
x is the raw score
m is the mean
s is the standard deviation in this case.
you get z = (128.6 - 148.3) / 92.3 = -.2134344529.
if you use a z-score calculator to get the probability of getting a z-score less than -.2134344529, the calculator will tell you that the probability is equal to .4154940862.
that would be your solution if you were talking about a raw score of 128.6.
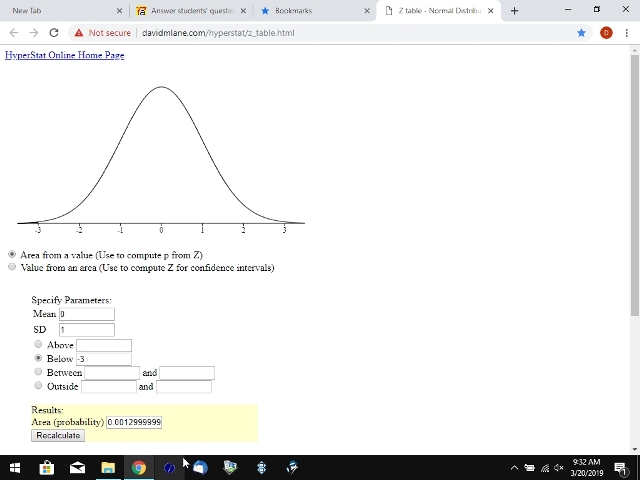
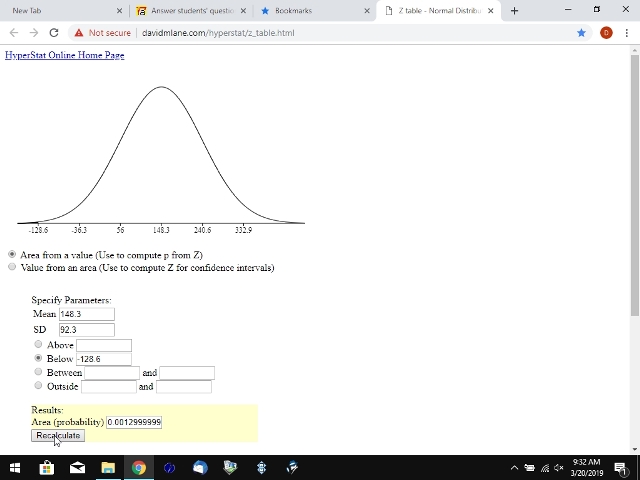
if you are talking about a raw score of minus 128.6, you would get a totally different answer.
in that case, z = (-128.6 - 148.3) / 92.3 gets you z = -3.
if you use a z-score calculator to get the probability of getting a z-score less than -3, the calculator will tell you that the probability is equal to
.0013499672.
i used the normal distribution calculator in the TI-84 Plus to get these numbers.
there is an online calculator that will do the calculations for you and give you a visual display of the results.
it does round a bit more than the TI-84 Plus, but the answer will be reasonably close if you take the rounding into consideration.
that calculator can be found at and the results of the analysis are shown below.
the calculator can be used with z-score or it can be used with raw scores.
if used with z-scores, the mean is 0 and the standard deviation is 1.
if used with raw scores, the mean is the actual mean and the standard deviation is the actual standard deviation.
i used the area from a value part of the calculator and i did z-scores first and then raw scores to show you the difference and the fact that you get the same answer give or take a few due to possible rounding differences.