p = the proportion of successes
q = the proportion of failures = 1 minus the proportion of successes
n = total number of observations = sample size
the formulas to use are:
p = .48 = proportion of successes
q = 1 - .48 = .52 = proportion of failures
mean = p
standard error = sqrt(p*q/n)
z = (x-m)/s
x = raw score
m = raw mean
s = standard error
90% degree of confidence results in a z-score of plus or minus 1.644853626 when using the TI-84 Plus scientific calculator.
90% confidence interval results in an alpha o
the alpha is the area under the normal distribution curve which is outside the confidence interval.
look for the z-score that has an area of .05 to the left of it gives you the negative critical z-score.
look for the z-score that has an area of .95 to the left of it gives you the positive critical z-score.
a z-score that has an area of.95 to the left of it is the same as a z-score that has an area of .05 to the right of it.
in your problem:
m is the mean which is equal to p which is equal to .48
n is the sample size which is equal to 200
s is the standard error which is equal to sqrt(p*q/n) which is equal to sqrt(.48*.52/200) which is equal to .0353270435
critical low z-score is equal to -1.644853626
critical high z-score is equal to 1.644853626
to find the low raw score, you use z=(x-m)/s which becomes -1.644853626 = (x-.48)/.0353270435.
solve for x to get x = z*s+m which becomes x = -1.644853626 * .0353270435 + .48 which becomes x = .4218921845.
to find the high raw score, you use z=(x-m)/s which becomes 1.644853626 = ((x-.48)/.0353270435.
solve for x to get x = 1*s+m which becomes x = 1.644853624 * .0353270435 + .48 which becomes x = .5381078155.
your 90% confident estimate of the population proportion is equal to anywhere between .4218921845 and .5381078155.
you would round as required.
visually this would look like the following.
first with z-scores
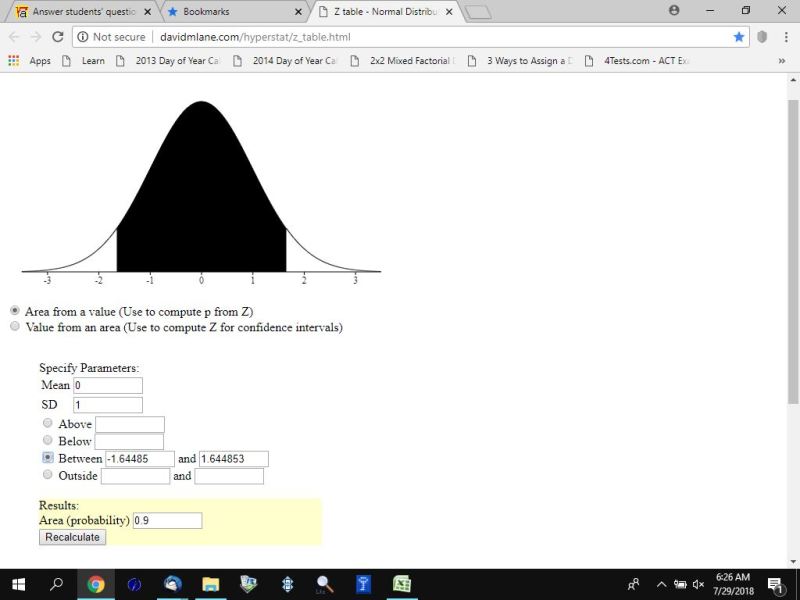
next with raw scores

the area shown at the bottom of each display is your confidence level which is equal to .9 = 90%.