using the following online normal distribution calculator, the z-score will be plus or minus 1.645.
this is essentially the same z-score except rounded to 3 decimal digits.
http://davidmlane.com/hyperstat/z_table.html
here's a picture of what i did using that calculator.

here's another calculator that i used.
http://stattrek.com/online-calculator/normal.aspx
here's a picture of what i did using that calculator.
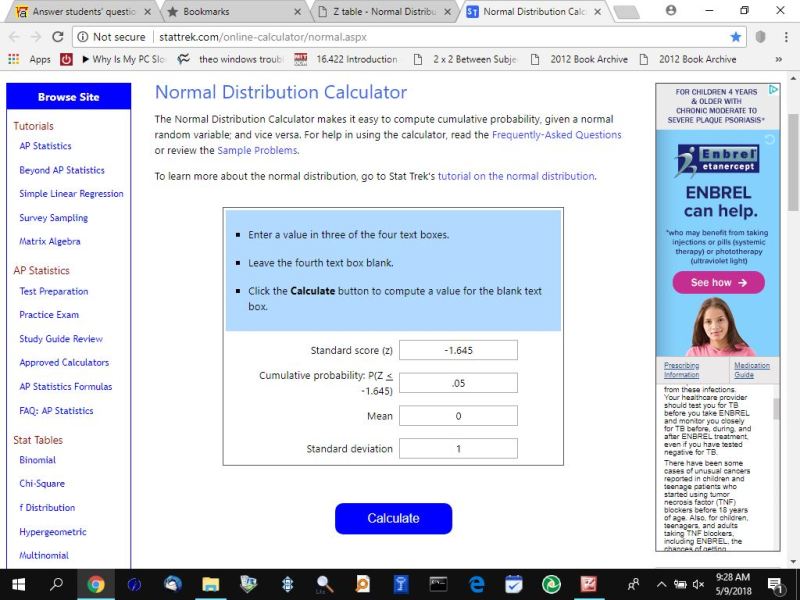
this calculator is used more like you would do when looking at a z-score table.
90% confidence limit means 10% is outside the limits.
divide this in half and you have 5% outside the limits to the left and 5% outside the limits to the right.
enter .05 area in the calculator and it will tell you that the z-score is -1.645.
that tells you that the area to the left of the z-score of -1.645 is equal to .05.
using the z-score table, you do essentially the same thing, only you can't tell it .05.
you have to look for an area of .05.
the table i used is at http://users.stat.ufl.edu/~athienit/Tables/Ztable.pdf
look up an area of .05 in the z-score table and you will see that .05 is not in the table.
you will see an area of .0505 and an area of .0495.
the z-score for .0505 is -1.64.
the z-score for .0495 is -1.65.
the z-score you are looking for is halfway between at -1.645.
here's a picgture of what i looked for.
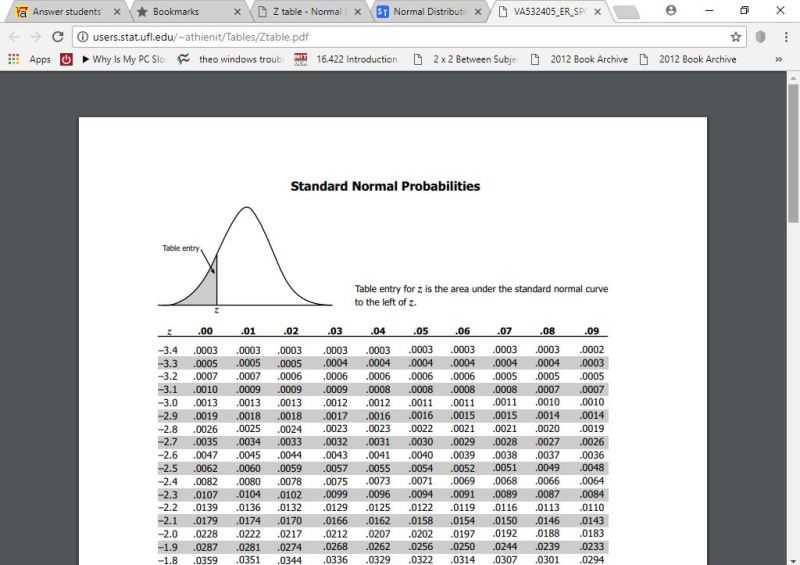
here's the specific line where i found the values i was looking for.

the first decimal place of the z-score is in the left hand column of the row that .0505 and .0495 are on.
the second decimal place of the z-score is in the first row of the column that .0505 and .0495 are on.
you will see .04 in the first row of the column that .0505 is in.
you will see .05 in the first row of the column that .0495 is in.
-1.6 + .04 equals -1.64
-1.6 + .05 equals -1.65