if you use a standard z-score table, you would look for an area to the left of a z-score that is closest to .559.
you would probably find that .5557 = .14 and .5596 = .15
since .5596 is closer to .559 than .5557, you would go with z = .15
there are online calculator that would get you the inverse.
one such calculator can be found at http://stattrek.com/online-calculator/normal.aspx
give it the area to the left of the z-score and it will tell you the z-score.
the table i used can be found at http://www.stat.ufl.edu/~athienit/Tables/Ztable.pdf
here's a picture of what i found.
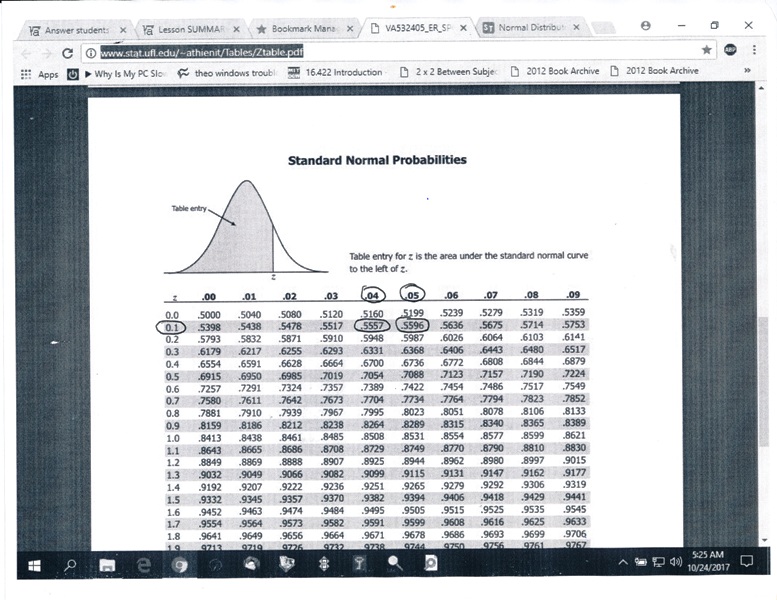
the areas to the left of the z-score are .5557 and .5596.
the row that they are on shows a z-score of .1
the columns that they are on show z-scores of .04 and .05
you add .1 to .04 and you get .14
you add .1 to .05 and you get .15
.15 has the area to the left of the z-score that is closest to .559, therefore choose .15.
if you want better accuracy, you can interpolate manually or use a calculator.
most times rounding to the nearest 2 decimal digits on the z-score is good enough.
a manual interpolation is not quite as accurate as a calculator generated result, but it gets you closer than you would have been otherwise.
a manual interpolation of what this table shows would get you the following.
.5557 to .559 is equal to .0033
.5557 to .5596 is equal to .0039
.0033 / .0039 = .8461538462
.14 to .15 = .01
.8461538462 * .01 = .008415385
.14 + .008415385 = .148415385 rounded to 3 decimal places = .148
your manual approximation would be .148 which is pretty close to what the calculator would have given you.
so, you would either go with .15 or with .148, depending on the accuracy required.
visually, your area to the left of the z-score of .148 would look like this:
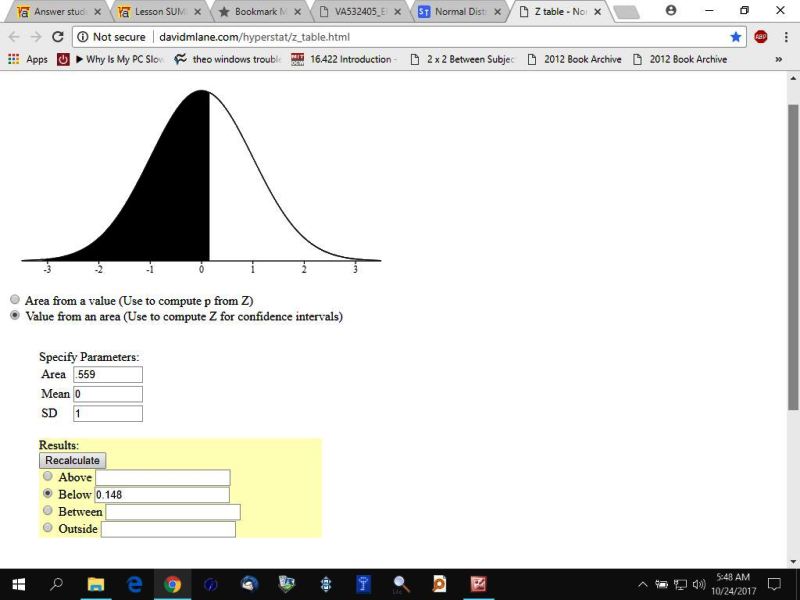
this is through the use of another calculator by david m. lane that gets your results and gives you a visual of what it looks like.
that calculator can be found at http://davidmlane.com/hyperstat/z_table.html