the population proportion is .23 (given)
the sample proportion is .27 (54/200 = .27)
the standard error of your test is sqrt(.23 * .77 / 200) = .029757352
your z-score is (.27 - .23) / .029757352 = 1.344205625.
round this to 1.34 and look it up in the z-score table and you will find that your alpha is equal to 1 - .9099 = .0901
.0901 is your solution.
when you calculate the standard error of the test, you need to use the population proportion rather than the sample proportion.
that gets you the correct answer.
you also needed to round the z-score to 2 digits.
the general formula is:
pmp = population mean proportion
pmq = 1 minus population mean proportion
smp = sample mean proportion
se = standard error of the test.
ss = sample size
the formula for se is:
se = sqrt(pmp * pmq / ss)
the formula for z-score is:
z = (smp - pmp) / se
in your problem:
pmp = .23
smp = 54/200 = .27
pmq = 1 - .23 = .77
you first need to calculate the standard error of the test.
that formula is se = sqrt(pmp * pmq / ss) which becomes se = sqrt(.23 * .77 / 200) which becomes .029757352
once you find the standard error of the test, you then find the z-score.
that formula is z = (smp - pmp) / se which becomes z = (.27 - .23) / .029757352 which becomes 1.344205625.
here you had to round the z-score to 2 decimal digits which gave you z = 1.34
if you didn't round it, and used a calculator, you would have gotten something different from .0901 but close.
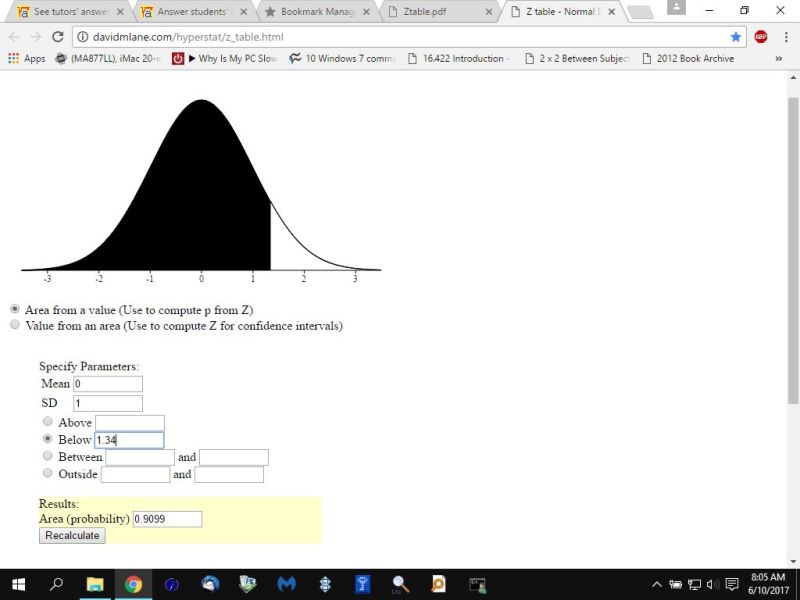
using the z-score table, 1.34 z-score gave you .9099 proportion of the normal distribution curve to the left of that z-score.
your alpha is the proportion of the distribution curve to the right of that z-score, which you obtain by subtracting .9099 from 1 to get .0901.
visually, it looks like this:
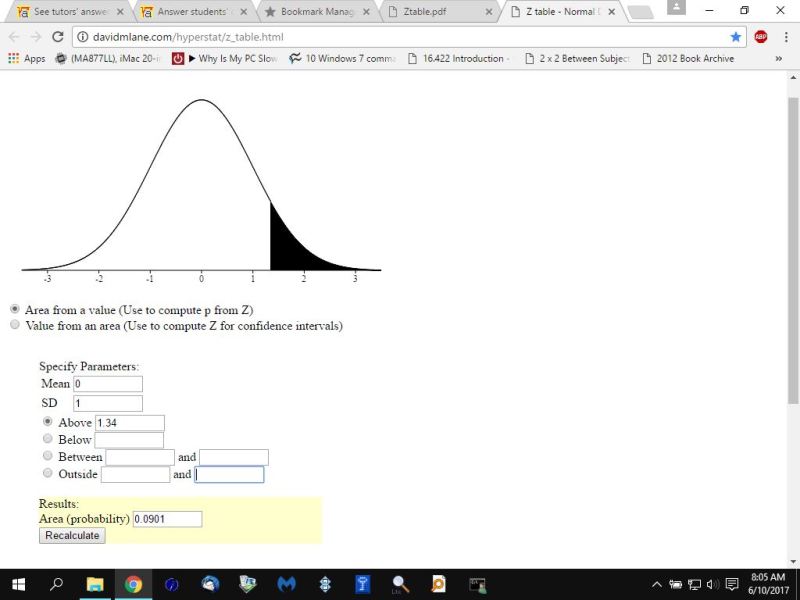
which is 1 minus what looks like this:
in the first picture i was looking for the area of the normal distribution curve above the z-core of 1.34 which is the same as looking for the area to the right of the z-score.
in the second picture i was looking for the area of the normal distribution curve below the z-score of 1.34 which is the same as looking for the area to the left of the z-score which is what the tables would normally show you.
to get the area to the right of the z-score, i had to subtract .9099 from 1 to get .0901.